Contents
- MLZ02_plot_dprime.m
- Get started
- Design parameters
- Load the data
- Quick-and-dirty plot of the individual-subject data
- Median response times, individual data
- Time- and condition-related variables -- See MLPilot02_params for details
- Group dprime plot:
- Plot group averaged d'
- Plot group d' by easy / hard delta
- Plot group d' for delta 11 (easy_dprime2)
- Plot group d' for delta 8 (hard_dprime2)
- Plot group d' for delta 11 (easy_dprime2)
- Sbj Order Learning Effect Scatter plot
- Group Order Learning Effect bar plot
- Group Order Learning Effect bar plot
- Main effect of Order on dprime:
- Group d'prime error plot
- Group criterion plot:
- Group RT plot
- Main effect of Order on RT
- Adjusted group RT plot
MLZ02_plot_dprime.m
Plot d' and RT learning curves for MLSecond02 experiment
File: work/MLExper/MLSecond02/prog/MLZ02_plot_dprime.m
Usage: publish('MLZ02_plot_dprime.m','html') ; % 'latex','doc','ppt'
Date: 2009-08-21% 1.0.2 2009-08-21 TH: Error bars on the group d' plot % 1.0.1 2009-07-25 AP: Minor tweaks % 1.0.0 2009-02-06 TH: Initial import to svn://orion/experiments/MLExper/
Get started
cd(fullfile(MLSecond02_pathstr,'data')) ; fprintf('\n\nMLZ02_plot_dprime executed on %s.\n\n',datestr(now)) ; fprintf('cd %s\n',pwd) ; clear all ;
MLZ02_plot_dprime executed on 01-Sep-2009 15:01:50. cd /Users/apetrov/a/r/w/work/MLExper/MLSecond02/data
Design parameters
Load them from the code that administered the experiment:
P = MLZ02_params(0) ; design_params = P.design_params ; N_sessions = design_params.max_session ; % 6 sessions blocks_session = design_params.blocks_session ; % 8 blocks per session N_blocks = N_sessions * blocks_session ; trials_block = design_params.trials_block ; % 104 trials per block N_trials = N_blocks * trials_block ; group_descr = {'1stN','2ndN','1stP','2ndP'} ; deltas = design_params.deltas ; % [11 8] = [easy difficult]
Load the data
filename = fullfile(MLSecond02_pathstr,'data','H.mat') ; %recalculatep = true ; recalculatep = false ; if (recalculatep || ~exist(filename,'file')) %- Write down repository revision number fprintf('!/usr/local/bin/svn info \n') ; !/usr/local/bin/svn info %- Concatenate the individual data files into one master ASCII file fprintf('!cat sbj*.dat > raw_data.dat \n') ; !cat sbj*.dat > raw_data.dat %- Import to Matlab fprintf('\nD=import_MLZ02_data ...') ; D=import_MLZ02_data(fullfile(MLSecond02_pathstr,'data','raw_data.dat')) ; %- Calculate d-primes fprintf('\nH = MLZ02_hitcount(D) ...\n') ; [H,P] = MLZ02_hitcount(D,1,P) ; save(filename,'H') ; fprintf('\nsave %s \n\n',filename) ; else fprintf('load %s \n\n',filename) ; load(filename) ; end % Used to factor out anomalous sbjs data comment out if you want % non-adjusted H values % adj_H- Adjusted H that modifies the following sbjs data % 1. Sbj 334 anomalous RT block during session 3 block 5-6 % Adjustment = Subtract constant % 2. Sbj 316 anomalous RT all of session 6 % Adjustment = Subtract 600, divide by 3, add 600 % 3. Sbj 325 anomalous d prime all of session 3 % Adjustment = Add constant % Set adj_H equal to H adj_H = H; % Make adjustment for sbj 334 alter RT_descr(don't change STD) % replace in adj_H idx = adj_H(1,16).RT_descr(21:22,1:7)-200; idx(1:2,2) = idx(1:2,2)+200; adj_H(1,16).RT_descr(21:22,1:7) = idx; % Make adjustment for sbj 316 alter RT_descr(don't change STD) and replace % in adj_H idx = ((adj_H(1,5).RT_descr(41:48,1) -600)./3)+600; idx2 = adj_H(1,5).RT_descr(41:48,2); idx3 = ((adj_H(1,5).RT_descr(41:48,3:7) -600)./3)+600; idx4 = zeros(8,7); idx4(1:8,1) = idx; idx4(1:8,2) = idx2; idx4(1:8,3:7) = idx3; adj_H(1,5).RT_descr(41:48,1:7) = idx4; % Make adjustment for sbj 325 alter all_dprime2 and replace in adj_H idx = adj_H(1,11).all_dprime2(9:12,1)+.95; adj_H(1,11).all_dprime2(9:12,1) = idx; % Set H equal to adj_H H = adj_H;
load /Users/apetrov/a/r/w/work/MLExper/MLSecond02/data/H.mat
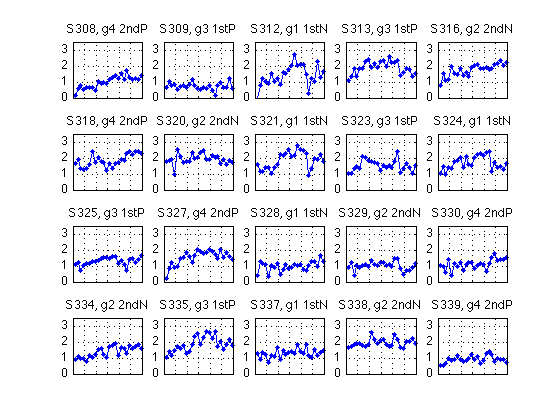
Quick-and-dirty plot of the individual-subject data
N_sbj = length(H) ; [r,c] = recommend_subplot_size(N_sbj) ; M = 3.5 ; for k=1:N_sbj subplot(r,c,k) ; plot(H(k).block2,H(k).all_dprime2,'b.-'); hold on; % plot(H(k).block2,H(k).easy_dprime2,'m--',... %1:5 pure 6:19 mixed 20:25pure % H(k).block2,H(k).hard_dprime2,'g--') ; %26:28 mixed axis([0 N_blocks 0 M]) ; grid on ; set(gca,'xtick',(0:blocks_session:N_blocks),'xticklabel',[],'ytick',(0:ceil(M))) ; gr1 = H(k).group ; title(sprintf('S%d, g%d %s',H(k).sbj,gr1,group_descr{gr1})) ; end gr = [H.group] ; xtab1(gr')
Value Count Percent Cum_cnt Cum_pct
-------------------------------------------
1 5 25.00 5 25.00
2 5 25.00 10 50.00
3 5 25.00 15 75.00
4 5 25.00 20 100.00
-------------------------------------------
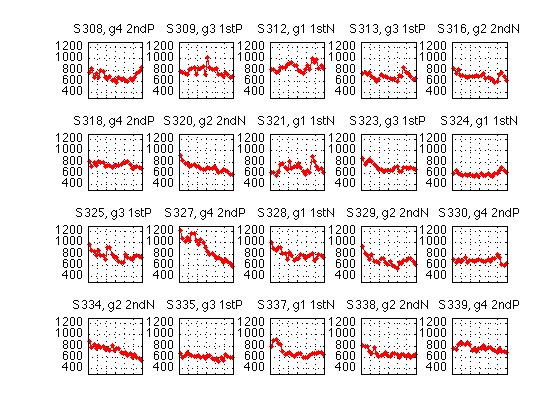
Median response times, individual data
clf M = 1300 ; % msec m = 300 ; for k=1:N_sbj subplot(r,c,k) ; idx = (2:2:H(k).N) ; RT_descr = H(k).RT_descr ; medianRT2 = (RT_descr(idx-1,5)+RT_descr(idx,5))./2 ; plot(H(k).block2,medianRT2,'r.-') ; axis([0 N_blocks m M]) ; grid on ; %ylabel('median RT') ; set(gca,'xtick',(0:blocks_session:N_blocks),'xticklabel',[]) ; gr1 = H(k).group ; title(sprintf('S%d, g%d %s',H(k).sbj,gr1,group_descr{gr1})) ; end % Discard incomplete data sets and pack the dprime2 field into a matrix N = [H(:).N] ; full_H = H ; H = H(N==N_blocks) ; N_sbj = length(H) ; [r,c] = recommend_subplot_size(N_sbj) ; gr = [H.group] ; xtab1(gr') dpr2 = [H.all_dprime2] ; % [N_blocks/2 x N_subjects] crit2 = [H.all_crit2] ; easy2= [H.easy_dprime2] ; ecrit2= [H.easy_crit2] ; hard2= [H.hard_dprime2] ; hcrit2= [H.hard_crit2] ; RT_descr=cat(3,H.RT_descr) ; % [N_blocks x 7 x N_subjects] medianRT = squeeze(RT_descr(:,5,:)) ; % [N_blocks x N_subjects] idx = 2:2:N_blocks ; medianRT2 = (medianRT(idx-1,:)+medianRT(idx,:))./2 ;
Value Count Percent Cum_cnt Cum_pct
-------------------------------------------
1 5 25.00 5 25.00
2 5 25.00 10 50.00
3 5 25.00 15 75.00
4 5 25.00 20 100.00
-------------------------------------------
Time- and condition-related variables -- See MLPilot02_params for details
bl = H(1).block2 ; % [28x1], blocks aggregated two by two
globalT = (bl-.5) .* trials_block ;
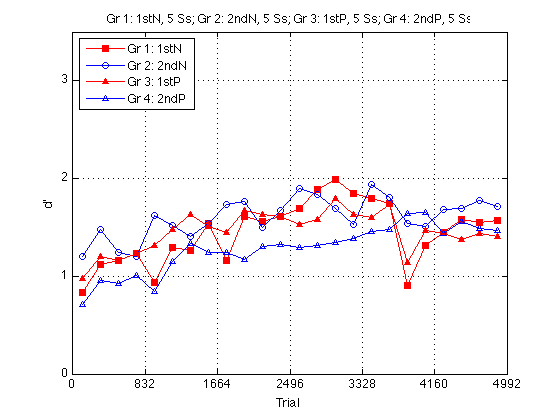
Group dprime plot:
Ss = cell(4,1) ;
l = {'Gr 1: 1stN','Gr 2: 2ndN','Gr 3: 1stP','Gr 4: 2ndP'} ;
for k = 1:4
Ss{k} = find(gr==k) ;
mdpr2(:,k) = mean(dpr2(:,Ss{k}),2) ; % average over subjects
mcrit2(:,k) = mean(crit2(:,Ss{k}),2) ;
mRT2(:,k) = mean(medianRT2(:,Ss{k}),2) ;
measy2(:,k) = mean(easy2(:,Ss{k}),2) ;
mhard2(:,k) = mean(hard2(:,Ss{k}),2) ;
end
assert(isempty(intersect(Ss{1},Ss{2}))) ; % Sanity check
assert(isempty(intersect(Ss{2},Ss{3}))) ; % Sanity check
assert(isempty(intersect(Ss{3},Ss{4}))) ; % Sanity check
clf
M = 3.5 ;
plot(globalT,mdpr2(:,1),'rs-',...
globalT,mdpr2(:,2),'bo-',...
globalT,mdpr2(:,3),'r^-',...
globalT,mdpr2(:,4),'b^-') ;
axis([0 N_trials 0 M]) ; grid on ;
set(findobj(gca,'Color','r'),'MarkerFaceColor','r') ;
set(gca,'xtick',(0:blocks_session:N_blocks)*trials_block,'ytick',(0:ceil(M))) ;
xlabel('Trial') ; ylabel('d''') ;
title(sprintf('%s, %d Ss; %s, %d Ss; %s, %d Ss; %s, %d Ss',...
l{1},length(Ss{1}),l{2},length(Ss{2}),...
l{3},length(Ss{3}),l{4},length(Ss{4}))) ;
legend(l,'location','NorthWest') ;
Plot group averaged d'
gr = [H.group] ; order1 = H(5).order2 ; order2 = H(1).order2 ; % Create a single averaged 28 x 1 matrix for gr 1+3 gr 2+4 and gr 1+2+3+4 % Group Averages all_dprime2 g13 = (mdpr2(:,1) + mdpr2(:,3)) / 2 ; g24 = (mdpr2(:,2) + mdpr2(:,4)) / 2 ; %g1234 = (mdpr2(:,1) + mdpr2(:,2) + mdpr2(:,3) + mdpr2(:,4)) / 4 ; % Group Averages easy_dprime2 and hard_dprime2 g13easy = (measy2(:,1) + measy2(:,3)) / 2 ; g13hard = (mhard2(:,1) + mhard2(:,3)) / 2 ; g24easy = (measy2(:,2) + measy2(:,4)) / 2 ; g24hard = (mhard2(:,2) + mhard2(:,4)) / 2 ; pre_test = (1:4)' ; % pre-test blocks pre_tn = (3:4)' ; % pre-test training order pre_tf = (1:2)' ; % pre-test transfer order post_test = (17:20)' ; % post-test blocks post_tn = (17:18)' ; % post-test training order post_tf = (19:20)' ; % post-test transfer order tn = (3:18)' ; % train in respective order tn_opp = (19:24)' ; % train opposite order globalT = (bl-.5)*trials_block ; % Loop to find the mean d_prime for all subjects in block2 for k=1:N_sbj x(k) = mean(H(k).all_dprime2); end; % Loop that subtracts the mean from each point in all_dprime2 % Sets all sbj mean dprime to zero % 20 subjects x 24 adjusted dprime values for k=1:20 U(k,:) = H(k).all_dprime2(:) - x(k); end % Separate into train first and train second groups / create index gr = [H.group]; gr = gr'; idx1 = find(gr==1 | gr==3); idx2 = find(gr==2 | gr==4); U1 = U(idx1,:); U2 = U(idx2,:); % Loop to compute standard error for each block for group1 for k=1:24 E(k) = std(U1(:,k)); ER1(k) = E(k)/sqrt(10); end % Loop to compute standard error for each block for group2 for k=1:24 E(k) = std(U2(:,k)); ER2(k) = E(k)/sqrt(10); end JTR = 10 ; % horizontal jitter [in trials] for visibility plot(-1,-1,'ks',-1,-1,'ko',-1,1,'rs',-1,1,'bo',... % for the legend globalT(pre_tn)-JTR,g13(pre_tn),'rs',... globalT(pre_tf)-JTR,g13(pre_tf),'ro',... globalT(pre_tn)+JTR,g24(pre_tn),'bs',... globalT(pre_tf)+JTR,g24(pre_tf),'bo',... globalT(tn)-JTR,g13(tn),'rs-',... globalT(tn)+JTR,g24(tn),'bs-',... globalT(post_tn)-JTR,g13(post_tn),'rs',... globalT(post_tf)-JTR,g13(post_tf),'ro',... globalT(post_tn)+JTR,g24(post_tn),'bs',... globalT(post_tf)+JTR,g24(post_tf),'bo',... globalT(tn_opp)-JTR,g13(tn_opp),'ro-',... globalT(tn_opp)+JTR,g24(tn_opp),'bo-') ; hold on ; errorbar1(globalT-JTR,g13,ER1,'rn'); hold off hold on ; errorbar1(globalT+JTR,g24,ER2,'bn'); hold off M = 2.5 ; axis([0 N_trials 0 M]) ; grid on ; set(gca,'xtick',(0:blocks_session:N_blocks)*trials_block,'ytick',(0:ceil(M))) ; set(findobj(gca,'Color','r'),'MarkerFaceColor','r'); %set(findobj(gca,'Color','g'),'MarkerFaceColor','g'); xlabel('Trial') ; ylabel('d''') ; %title(sprintf('Group Average Pre/Post-Test, Train, and Train Opposite')); legend('Training order','Transfer order','1st order groups','2nd order groups','Location','NorthWest') ; title(sprintf('MLSecond02: Groups 1+3 (%d Ss) and 2+4 (%d Ss)',... length(Ss{1})+length(Ss{3}), length(Ss{2})+length(Ss{4}))) ;
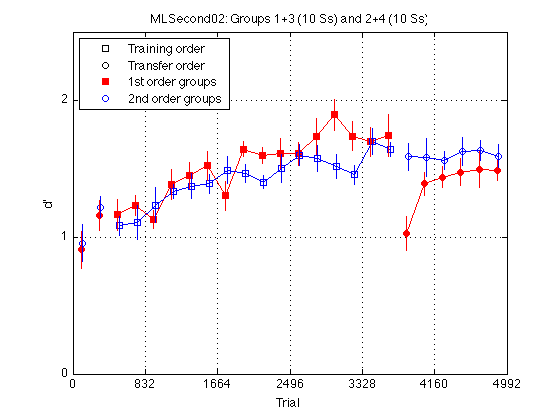
Plot group d' by easy / hard delta
gr = [H.group] ; order1 = H(5).order2 ; order2 = H(1).order2 ; % Create a single averaged 28 x 1 matrix for gr 1+3 gr 2+4 and gr 1+2+3+4 % Group Averages all_dprime2 g13 = (mdpr2(:,1) + mdpr2(:,3)) / 2 ; g24 = (mdpr2(:,2) + mdpr2(:,4)) / 2 ; %g1234 = (mdpr2(:,1) + mdpr2(:,2) + mdpr2(:,3) + mdpr2(:,4)) / 4 ; % Group Averages easy_dprime2 and hard_dprime2 g13easy = (measy2(:,1) + measy2(:,3)) / 2 ; g13hard = (mhard2(:,1) + mhard2(:,3)) / 2 ; g24easy = (measy2(:,2) + measy2(:,4)) / 2 ; g24hard = (mhard2(:,2) + mhard2(:,4)) / 2 ; pre_test = (1:4)' ; % pre-test blocks pre_tn = (3:4)' ; % pre-test training order pre_tf = (1:2)' ; % pre-test transfer order post_test = (17:20)' ; % post-test blocks post_tn = (17:18)' ; % post-test training order post_tf = (19:20)' ; % post-test transfer order tn = (3:18)' ; % train in respective order tn_opp = (19:24)' ; % train opposite order globalT = (bl-.5)*trials_block ; %%Plot the group-averaged d' clf M = 3.5 ; plot(-1,-1,'ks',-1,-1,'ko',-1,-1,'k-',-1,-1,'k--',... -1,1,'rs',-1,1,'bo',... % for the legend globalT(pre_tn),g13easy(pre_tn),'rs',... globalT(pre_tn),g13hard(pre_tn),'rs--',... globalT(pre_tf),g13easy(pre_tf),'ro',... globalT(pre_tf),g13hard(pre_tf),'ro--',... globalT(pre_tn),g24easy(pre_tn),'bs',... globalT(pre_tn),g24hard(pre_tn),'bs--',... globalT(pre_tf),g24easy(pre_tf),'bo',... globalT(pre_tf),g24hard(pre_tf),'bo--',... globalT(tn),g13easy(tn),'rs-',... globalT(tn),g13hard(tn),'rs--',... globalT(tn),g24easy(tn),'bs-',... globalT(tn),g24hard(tn),'bs--',... globalT(post_tn),g13easy(post_tn),'rs',... globalT(post_tn),g13hard(post_tn),'rs--',... globalT(post_tf),g13easy(post_tf),'ro',... globalT(post_tf),g13hard(post_tf),'ro--',... globalT(post_tn),g24easy(post_tn),'bs',... globalT(post_tn),g24hard(post_tn),'bs--',... globalT(post_tf),g24easy(post_tf),'bo',... globalT(post_tf),g24hard(post_tf),'bo--',... globalT(tn_opp),g13easy(tn_opp),'ro-',... globalT(tn_opp),g13hard(tn_opp),'ro--',... globalT(tn_opp),g24easy(tn_opp),'bo-',... globalT(tn_opp),g24hard(tn_opp),'bo--') axis([0 N_trials 0 M]) ; grid on ; set(gca,'xtick',(0:blocks_session:N_blocks)*trials_block,'ytick',(0:ceil(M))) ; set(findobj(gca,'Color','r'),'MarkerFaceColor','r'); %set(findobj(gca,'Color','g'),'MarkerFaceColor','g'); xlabel('Trial') ; ylabel('d''') ; legend('Training order','Transfer order','Easy delta','Diff delta',... '1st order groups','2nd order groups','Location','NorthWest') ; % %% Plot group d' at half temporal resolution % idx2 = 2:2:24 ; % % g13easy2 = (g13easy(idx2-1) + g13easy(idx2))./2 ; % g13hard2 = (g13hard(idx2-1) + g13hard(idx2))./2 ; % g24easy2 = (g24easy(idx2-1) + g24easy(idx2))./2 ; % g24hard2 = (g24hard(idx2-1) + g24hard(idx2))./2 ; % % globalT2 = (globalT(idx2-1) + globalT(idx2))./2 ; % % pre_test2 = (1:2)' ; % pre-test blocks % pre_tn2 = (2)' ; % pre-test training order % pre_tf2 = (1)' ; % pre-test transfer order % post_test2 = (9:10)' ; % post-test blocks % post_tn2 = (9)' ; % post-test training order % post_tf2 = (10)' ; % post-test transfer order % tn2 = (2:9)' ; % train in respective order % tn_opp2 = (10:12)' ; % train opposite order % % %%Plot the smoothed group-averaged d' % clf % M = 3.0 ; % plot(-1,-1,'ks',-1,-1,'ko',-1,-1,'k-',-1,-1,'k--',... % -1,1,'rs',-1,1,'bo',... % for the legend % globalT2(pre_tn2),g13easy2(pre_tn2),'rs',... % globalT2(pre_tn2),g13hard2(pre_tn2),'rs--',... % globalT2(pre_tf2),g13easy2(pre_tf2),'ro',... % globalT2(pre_tf2),g13hard2(pre_tf2),'ro--',... % globalT2(pre_tn2),g24easy2(pre_tn2),'bs',... % globalT2(pre_tn2),g24hard2(pre_tn2),'bs--',... % globalT2(pre_tf2),g24easy2(pre_tf2),'bo',... % globalT2(pre_tf2),g24hard2(pre_tf2),'bo--',... % globalT2(tn2),g13easy2(tn2),'rs-',... % globalT2(tn2),g13hard2(tn2),'rs--',... % globalT2(tn2),g24easy2(tn2),'bs-',... % globalT2(tn2),g24hard2(tn2),'bs--',... % globalT2(post_tn2),g13easy2(post_tn2),'rs',... % globalT2(post_tn2),g13hard2(post_tn2),'rs--',... % globalT2(post_tf2),g13easy2(post_tf2),'ro',... % globalT2(post_tf2),g13hard2(post_tf2),'ro--',... % globalT2(post_tn2),g24easy2(post_tn2),'bs',... % globalT2(post_tn2),g24hard2(post_tn2),'bs--',... % globalT2(post_tf2),g24easy2(post_tf2),'bo',... % globalT2(post_tf2),g24hard2(post_tf2),'bo--',... % globalT2(tn_opp2),g13easy2(tn_opp2),'ro-',... % globalT2(tn_opp2),g13hard2(tn_opp2),'ro--',... % globalT2(tn_opp2),g24easy2(tn_opp2),'bo-',... % globalT2(tn_opp2),g24hard2(tn_opp2),'bo--') % hold on % axis([0 N_trials 0 M]) ; grid on ; % set(gca,'xtick',(0:blocks_session:N_blocks)*trials_block,'ytick',(0:ceil(M))) ; % set(findobj(gca,'Color','r'),'MarkerFaceColor','r'); % %set(findobj(gca,'Color','g'),'MarkerFaceColor','g'); % xlabel('Trial') ; ylabel('d''') ; % %title(sprintf('Group Average Pre/Post-Test, Train, and Train Opposite (10 vs 6 delta split)')); % legend('Training order','Transfer order','Easy delta','Diff delta',... % '1st order groups','2nd order groups','Location','NorthWest') ;
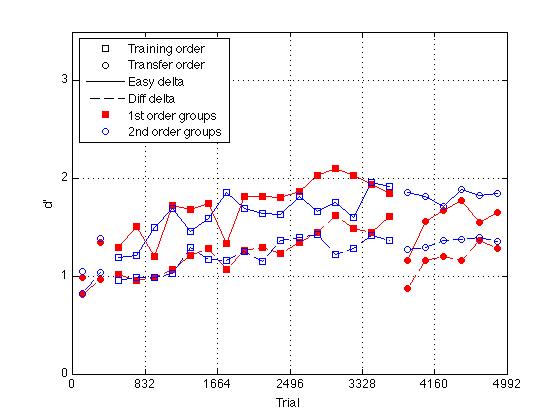
Plot group d' for delta 11 (easy_dprime2)
gr = [H.group] ; order1 = H(5).order2 ; order2 = H(1).order2 ; % Create a single averaged 28 x 1 matrix for gr 1+3 gr 2+4 and gr 1+2+3+4 % Group Averages all_dprime2 g13 = (mdpr2(:,1) + mdpr2(:,3)) / 2 ; g24 = (mdpr2(:,2) + mdpr2(:,4)) / 2 ; %g1234 = (mdpr2(:,1) + mdpr2(:,2) + mdpr2(:,3) + mdpr2(:,4)) / 4 ; % Group Averages easy_dprime2 and hard_dprime2 g13easy = (measy2(:,1) + measy2(:,3)) / 2 ; g13hard = (mhard2(:,1) + mhard2(:,3)) / 2 ; g24easy = (measy2(:,2) + measy2(:,4)) / 2 ; g24hard = (mhard2(:,2) + mhard2(:,4)) / 2 ; pre_test = (1:4)' ; % pre-test blocks pre_tn = (3:4)' ; % pre-test training order pre_tf = (1:2)' ; % pre-test transfer order post_test = (17:20)' ; % post-test blocks post_tn = (17:18)' ; % post-test training order post_tf = (19:20)' ; % post-test transfer order tn = (3:18)' ; % train in respective order tn_opp = (19:24)' ; % train opposite order globalT = (bl-.5)*trials_block ; % Loop to find the mean d_prime for all subjects in block2 for k=1:N_sbj x(k) = mean(H(k).easy_dprime2); end; % Loop that subtracts the mean from each point in all_dprime2 % Sets all sbj mean dprime to zero % 20 subjects x 24 adjusted dprime values for k=1:20 U(k,:) = H(k).easy_dprime2(:) - x(k); end % Separate into train first and train second groups / create index gr = [H.group]; gr = gr'; idx1 = find(gr==1 | gr==3); idx2 = find(gr==2 | gr==4); U1 = U(idx1,:); U2 = U(idx2,:); % Loop to compute standard error for each block for group1 for k=1:24 E(k) = std(U1(:,k)); ER1(k) = E(k)/sqrt(10); end % Loop to compute standard error for each block for group2 for k=1:24 E(k) = std(U2(:,k)); ER2(k) = E(k)/sqrt(10); end JTR = 10 ; % horizontal jitter [in trials] for visibility plot(-1,-1,'ks',-1,-1,'ko',-1,1,'rs',-1,1,'bo',... % for the legend globalT(pre_tn)-JTR,g13easy(pre_tn),'rs',... globalT(pre_tf)-JTR,g13easy(pre_tf),'ro',... globalT(pre_tn)+JTR,g24easy(pre_tn),'bs',... globalT(pre_tf)+JTR,g24easy(pre_tf),'bo',... globalT(tn)-JTR,g13easy(tn),'rs-',... globalT(tn)+JTR,g24easy(tn),'bs-',... globalT(post_tn)-JTR,g13easy(post_tn),'rs',... globalT(post_tf)-JTR,g13easy(post_tf),'ro',... globalT(post_tn)+JTR,g24easy(post_tn),'bs',... globalT(post_tf)+JTR,g24easy(post_tf),'bo',... globalT(tn_opp)-JTR,g13easy(tn_opp),'ro-',... globalT(tn_opp)+JTR,g24easy(tn_opp),'bo-') ; hold on ; errorbar1(globalT-JTR,g13easy,ER1,'rn'); hold off hold on ; errorbar1(globalT+JTR,g24easy,ER2,'bn'); hold off M = 2.5 ; axis([0 N_trials 0 M]) ; grid on ; set(gca,'xtick',(0:blocks_session:N_blocks)*trials_block,'ytick',(0:ceil(M))) ; set(findobj(gca,'Color','r'),'MarkerFaceColor','r'); %set(findobj(gca,'Color','g'),'MarkerFaceColor','g'); xlabel('Trial') ; ylabel('d''') ; %title(sprintf('Group Average Pre/Post-Test, Train, and Train Opposite')); legend('Training order','Transfer order','1st order groups','2nd order groups','Location','NorthWest') ; % %% Plot group d' at half temporal resolution % idx2 = 2:2:24 ; % % g13easy2 = (g13easy(idx2-1) + g13easy(idx2))./2 ; % g13hard2 = (g13hard(idx2-1) + g13hard(idx2))./2 ; % g24easy2 = (g24easy(idx2-1) + g24easy(idx2))./2 ; % g24hard2 = (g24hard(idx2-1) + g24hard(idx2))./2 ; % % globalT2 = (globalT(idx2-1) + globalT(idx2))./2 ; % % pre_test2 = (1:2)' ; % pre-test blocks % pre_tn2 = (2)' ; % pre-test training order % pre_tf2 = (1)' ; % pre-test transfer order % post_test2 = (9:10)' ; % post-test blocks % post_tn2 = (9)' ; % post-test training order % post_tf2 = (10)' ; % post-test transfer order % tn2 = (2:9)' ; % train in respective order % tn_opp2 = (10:12)' ; % train opposite order % % %%Plot the smoothed group-averaged d' % clf % M = 3.0 ; % plot(-1,-1,'ks',-1,-1,'ko',-1,-1,'k-',-1,-1,'k--',... % -1,1,'rs',-1,1,'bo',... % for the legend % globalT2(pre_tn2),g13easy2(pre_tn2),'rs',... % globalT2(pre_tn2),g13hard2(pre_tn2),'rs--',... % globalT2(pre_tf2),g13easy2(pre_tf2),'ro',... % globalT2(pre_tf2),g13hard2(pre_tf2),'ro--',... % globalT2(pre_tn2),g24easy2(pre_tn2),'bs',... % globalT2(pre_tn2),g24hard2(pre_tn2),'bs--',... % globalT2(pre_tf2),g24easy2(pre_tf2),'bo',... % globalT2(pre_tf2),g24hard2(pre_tf2),'bo--',... % globalT2(tn2),g13easy2(tn2),'rs-',... % globalT2(tn2),g13hard2(tn2),'rs--',... % globalT2(tn2),g24easy2(tn2),'bs-',... % globalT2(tn2),g24hard2(tn2),'bs--',... % globalT2(post_tn2),g13easy2(post_tn2),'rs',... % globalT2(post_tn2),g13hard2(post_tn2),'rs--',... % globalT2(post_tf2),g13easy2(post_tf2),'ro',... % globalT2(post_tf2),g13hard2(post_tf2),'ro--',... % globalT2(post_tn2),g24easy2(post_tn2),'bs',... % globalT2(post_tn2),g24hard2(post_tn2),'bs--',... % globalT2(post_tf2),g24easy2(post_tf2),'bo',... % globalT2(post_tf2),g24hard2(post_tf2),'bo--',... % globalT2(tn_opp2),g13easy2(tn_opp2),'ro-',... % globalT2(tn_opp2),g13hard2(tn_opp2),'ro--',... % globalT2(tn_opp2),g24easy2(tn_opp2),'bo-',... % globalT2(tn_opp2),g24hard2(tn_opp2),'bo--') % hold on % % axis([0 N_trials 0 M]) ; grid on ; % set(gca,'xtick',(0:blocks_session:N_blocks)*trials_block,'ytick',(0:ceil(M))) ; % set(findobj(gca,'Color','r'),'MarkerFaceColor','r'); % %set(findobj(gca,'Color','g'),'MarkerFaceColor','g'); % xlabel('Trial') ; ylabel('d''') ; % %title(sprintf('Group Average Pre/Post-Test, Train, and Train Opposite (10 vs 6 delta split)')); % legend('Training order','Transfer order','Easy delta','Diff delta',... % '1st order groups','2nd order groups','Location','NorthWest') ;
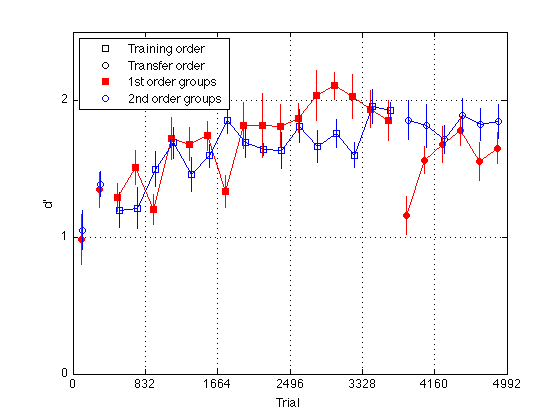
Plot group d' for delta 8 (hard_dprime2)
gr = [H.group] ; order1 = H(5).order2 ; order2 = H(1).order2 ; % Create a single averaged 28 x 1 matrix for gr 1+3 gr 2+4 and gr 1+2+3+4 % Group Averages all_dprime2 g13 = (mdpr2(:,1) + mdpr2(:,3)) / 2 ; g24 = (mdpr2(:,2) + mdpr2(:,4)) / 2 ; %g1234 = (mdpr2(:,1) + mdpr2(:,2) + mdpr2(:,3) + mdpr2(:,4)) / 4 ; % Group Averages easy_dprime2 and hard_dprime2 g13easy = (measy2(:,1) + measy2(:,3)) / 2 ; g13hard = (mhard2(:,1) + mhard2(:,3)) / 2 ; g24easy = (measy2(:,2) + measy2(:,4)) / 2 ; g24hard = (mhard2(:,2) + mhard2(:,4)) / 2 ; pre_test = (1:4)' ; % pre-test blocks pre_tn = (3:4)' ; % pre-test training order pre_tf = (1:2)' ; % pre-test transfer order post_test = (17:20)' ; % post-test blocks post_tn = (17:18)' ; % post-test training order post_tf = (19:20)' ; % post-test transfer order tn = (3:18)' ; % train in respective order tn_opp = (19:24)' ; % train opposite order globalT = (bl-.5)*trials_block ; % Loop to find the mean d_prime for all subjects in block2 for k=1:N_sbj x(k) = mean(H(k).hard_dprime2); end; % Loop that subtracts the mean from each point in all_dprime2 % Sets all sbj mean dprime to zero % 20 subjects x 24 adjusted dprime values for k=1:20 U(k,:) = H(k).hard_dprime2(:) - x(k); end % Separate into train first and train second groups / create index gr = [H.group]; gr = gr'; idx1 = find(gr==1 | gr==3); idx2 = find(gr==2 | gr==4); U1 = U(idx1,:); U2 = U(idx2,:); % Loop to compute standard error for each block for group1 for k=1:24 E(k) = std(U1(:,k)); ER1(k) = E(k)/sqrt(10); end % Loop to compute standard error for each block for group2 for k=1:24 E(k) = std(U2(:,k)); ER2(k) = E(k)/sqrt(10); end JTR = 10 ; % horizontal jitter [in trials] for visibility plot(-1,-1,'ks',-1,-1,'ko',-1,1,'rs',-1,1,'bo',... % for the legend globalT(pre_tn)-JTR,g13hard(pre_tn),'rs',... globalT(pre_tf)-JTR,g13hard(pre_tf),'ro',... globalT(pre_tn)+JTR,g24hard(pre_tn),'bs',... globalT(pre_tf)+JTR,g24hard(pre_tf),'bo',... globalT(tn)-JTR,g13hard(tn),'rs-',... globalT(tn)+JTR,g24hard(tn),'bs-',... globalT(post_tn)-JTR,g13hard(post_tn),'rs',... globalT(post_tf)-JTR,g13hard(post_tf),'ro',... globalT(post_tn)+JTR,g24hard(post_tn),'bs',... globalT(post_tf)+JTR,g24hard(post_tf),'bo',... globalT(tn_opp)-JTR,g13hard(tn_opp),'ro-',... globalT(tn_opp)+JTR,g24hard(tn_opp),'bo-') ; hold on ; errorbar1(globalT-JTR,g13hard,ER1,'rn'); hold off hold on ; errorbar1(globalT+JTR,g24hard,ER2,'bn'); hold off M = 2.5 ; axis([0 N_trials 0 M]) ; grid on ; set(gca,'xtick',(0:blocks_session:N_blocks)*trials_block,'ytick',(0:ceil(M))) ; set(findobj(gca,'Color','r'),'MarkerFaceColor','r'); %set(findobj(gca,'Color','g'),'MarkerFaceColor','g'); xlabel('Trial') ; ylabel('d''') ; %title(sprintf('Group Average Pre/Post-Test, Train, and Train Opposite')); legend('Training order','Transfer order','1st order groups','2nd order groups','Location','NorthWest') ; % %% Plot group d' at half temporal resolution % idx2 = 2:2:24 ; % % g13easy2 = (g13easy(idx2-1) + g13easy(idx2))./2 ; % g13hard2 = (g13hard(idx2-1) + g13hard(idx2))./2 ; % g24easy2 = (g24easy(idx2-1) + g24easy(idx2))./2 ; % g24hard2 = (g24hard(idx2-1) + g24hard(idx2))./2 ; % % globalT2 = (globalT(idx2-1) + globalT(idx2))./2 ; % % pre_test2 = (1:2)' ; % pre-test blocks % pre_tn2 = (2)' ; % pre-test training order % pre_tf2 = (1)' ; % pre-test transfer order % post_test2 = (9:10)' ; % post-test blocks % post_tn2 = (9)' ; % post-test training order % post_tf2 = (10)' ; % post-test transfer order % tn2 = (2:9)' ; % train in respective order % tn_opp2 = (10:12)' ; % train opposite order % % %%Plot the smoothed group-averaged d' % clf % M = 3.0 ; % plot(-1,-1,'ks',-1,-1,'ko',-1,-1,'k-',-1,-1,'k--',... % -1,1,'rs',-1,1,'bo',... % for the legend % globalT2(pre_tn2),g13easy2(pre_tn2),'rs',... % globalT2(pre_tn2),g13hard2(pre_tn2),'rs--',... % globalT2(pre_tf2),g13easy2(pre_tf2),'ro',... % globalT2(pre_tf2),g13hard2(pre_tf2),'ro--',... % globalT2(pre_tn2),g24easy2(pre_tn2),'bs',... % globalT2(pre_tn2),g24hard2(pre_tn2),'bs--',... % globalT2(pre_tf2),g24easy2(pre_tf2),'bo',... % globalT2(pre_tf2),g24hard2(pre_tf2),'bo--',... % globalT2(tn2),g13easy2(tn2),'rs-',... % globalT2(tn2),g13hard2(tn2),'rs--',... % globalT2(tn2),g24easy2(tn2),'bs-',... % globalT2(tn2),g24hard2(tn2),'bs--',... % globalT2(post_tn2),g13easy2(post_tn2),'rs',... % globalT2(post_tn2),g13hard2(post_tn2),'rs--',... % globalT2(post_tf2),g13easy2(post_tf2),'ro',... % globalT2(post_tf2),g13hard2(post_tf2),'ro--',... % globalT2(post_tn2),g24easy2(post_tn2),'bs',... % globalT2(post_tn2),g24hard2(post_tn2),'bs--',... % globalT2(post_tf2),g24easy2(post_tf2),'bo',... % globalT2(post_tf2),g24hard2(post_tf2),'bo--',... % globalT2(tn_opp2),g13easy2(tn_opp2),'ro-',... % globalT2(tn_opp2),g13hard2(tn_opp2),'ro--',... % globalT2(tn_opp2),g24easy2(tn_opp2),'bo-',... % globalT2(tn_opp2),g24hard2(tn_opp2),'bo--') % hold on % axis([0 N_trials 0 M]) ; grid on ; % set(gca,'xtick',(0:blocks_session:N_blocks)*trials_block,'ytick',(0:ceil(M))) ; % set(findobj(gca,'Color','r'),'MarkerFaceColor','r'); % %set(findobj(gca,'Color','g'),'MarkerFaceColor','g'); % xlabel('Trial') ; ylabel('d''') ; % %title(sprintf('Group Average Pre/Post-Test, Train, and Train Opposite (10 vs 6 delta split)')); % legend('Training order','Transfer order','Easy delta','Diff delta',... % '1st order groups','2nd order groups','Location','NorthWest') ;
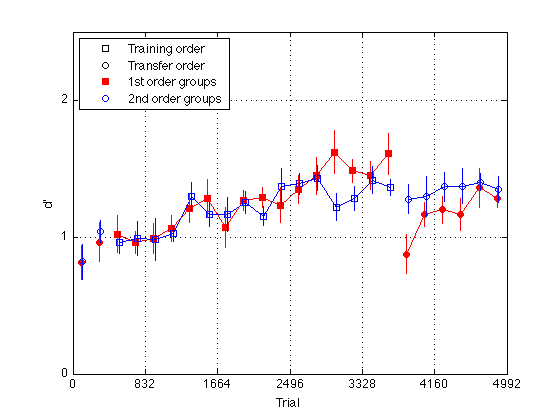
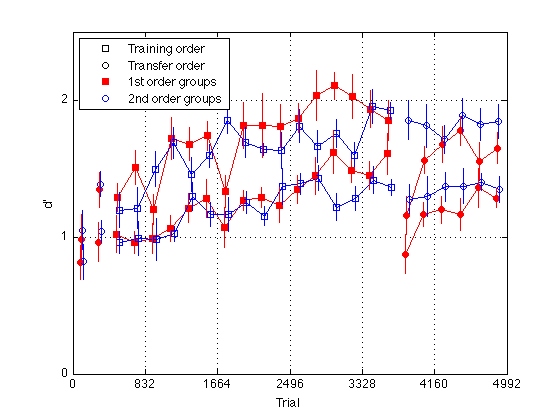
Plot group d' for delta 11 (easy_dprime2)
gr = [H.group] ; order1 = H(5).order2 ; order2 = H(1).order2 ; % Create a single averaged 28 x 1 matrix for gr 1+3 gr 2+4 and gr 1+2+3+4 % Group Averages all_dprime2 g13 = (mdpr2(:,1) + mdpr2(:,3)) / 2 ; g24 = (mdpr2(:,2) + mdpr2(:,4)) / 2 ; %g1234 = (mdpr2(:,1) + mdpr2(:,2) + mdpr2(:,3) + mdpr2(:,4)) / 4 ; % Group Averages easy_dprime2 and hard_dprime2 g13easy = (measy2(:,1) + measy2(:,3)) / 2 ; g13hard = (mhard2(:,1) + mhard2(:,3)) / 2 ; g24easy = (measy2(:,2) + measy2(:,4)) / 2 ; g24hard = (mhard2(:,2) + mhard2(:,4)) / 2 ; pre_test = (1:4)' ; % pre-test blocks pre_tn = (3:4)' ; % pre-test training order pre_tf = (1:2)' ; % pre-test transfer order post_test = (17:20)' ; % post-test blocks post_tn = (17:18)' ; % post-test training order post_tf = (19:20)' ; % post-test transfer order tn = (3:18)' ; % train in respective order tn_opp = (19:24)' ; % train opposite order globalT = (bl-.5)*trials_block ; % Loop to find the mean d_prime for all subjects in block2 for k=1:N_sbj x(k) = mean(H(k).easy_dprime2); end; % Loop that subtracts the mean from each point in all_dprime2 % Sets all sbj mean dprime to zero % 20 subjects x 24 adjusted dprime values for k=1:20 U(k,:) = H(k).easy_dprime2(:) - x(k); end % Separate into train first and train second groups / create index gr = [H.group]; gr = gr'; idx1 = find(gr==1 | gr==3); idx2 = find(gr==2 | gr==4); U1 = U(idx1,:); U2 = U(idx2,:); % Loop to compute standard error for each block for group1 for k=1:24 E(k) = std(U1(:,k)); ER1(k) = E(k)/sqrt(10); end % Loop to compute standard error for each block for group2 for k=1:24 E(k) = std(U2(:,k)); ER2(k) = E(k)/sqrt(10); end JTR = 10 ; % horizontal jitter [in trials] for visibility plot(-1,-1,'ks',-1,-1,'ko',-1,1,'rs',-1,1,'bo',... % for the legend globalT(pre_tn)-JTR,g13easy(pre_tn),'rs',... globalT(pre_tf)-JTR,g13easy(pre_tf),'ro',... globalT(pre_tn)+JTR,g24easy(pre_tn),'bs',... globalT(pre_tf)+JTR,g24easy(pre_tf),'bo',... globalT(tn)-JTR,g13easy(tn),'rs-',... globalT(tn)+JTR,g24easy(tn),'bs-',... globalT(post_tn)-JTR,g13easy(post_tn),'rs',... globalT(post_tf)-JTR,g13easy(post_tf),'ro',... globalT(post_tn)+JTR,g24easy(post_tn),'bs',... globalT(post_tf)+JTR,g24easy(post_tf),'bo',... globalT(tn_opp)-JTR,g13easy(tn_opp),'ro-',... globalT(tn_opp)+JTR,g24easy(tn_opp),'bo-') ; hold on ; errorbar1(globalT-JTR,g13easy,ER1,'rn'); hold off hold on ; errorbar1(globalT+JTR,g24easy,ER2,'bn'); hold off hold on ; % Plot group d' for delta 8 (hard_dprime2) gr = [H.group] ; order1 = H(5).order2 ; order2 = H(1).order2 ; % Create a single averaged 28 x 1 matrix for gr 1+3 gr 2+4 and gr 1+2+3+4 % Group Averages all_dprime2 g13 = (mdpr2(:,1) + mdpr2(:,3)) / 2 ; g24 = (mdpr2(:,2) + mdpr2(:,4)) / 2 ; %g1234 = (mdpr2(:,1) + mdpr2(:,2) + mdpr2(:,3) + mdpr2(:,4)) / 4 ; % Group Averages easy_dprime2 and hard_dprime2 g13easy = (measy2(:,1) + measy2(:,3)) / 2 ; g13hard = (mhard2(:,1) + mhard2(:,3)) / 2 ; g24easy = (measy2(:,2) + measy2(:,4)) / 2 ; g24hard = (mhard2(:,2) + mhard2(:,4)) / 2 ; pre_test = (1:4)' ; % pre-test blocks pre_tn = (3:4)' ; % pre-test training order pre_tf = (1:2)' ; % pre-test transfer order post_test = (17:20)' ; % post-test blocks post_tn = (17:18)' ; % post-test training order post_tf = (19:20)' ; % post-test transfer order tn = (3:18)' ; % train in respective order tn_opp = (19:24)' ; % train opposite order globalT = (bl-.5)*trials_block ; % Loop to find the mean d_prime for all subjects in block2 for k=1:N_sbj x(k) = mean(H(k).hard_dprime2); end; % Loop that subtracts the mean from each point in all_dprime2 % Sets all sbj mean dprime to zero % 20 subjects x 24 adjusted dprime values for k=1:20 U(k,:) = H(k).hard_dprime2(:) - x(k); end % Separate into train first and train second groups / create index gr = [H.group]; gr = gr'; idx1 = find(gr==1 | gr==3); idx2 = find(gr==2 | gr==4); U1 = U(idx1,:); U2 = U(idx2,:); % Loop to compute standard error for each block for group1 for k=1:24 E(k) = std(U1(:,k)); ER1(k) = E(k)/sqrt(10); end % Loop to compute standard error for each block for group2 for k=1:24 E(k) = std(U2(:,k)); ER2(k) = E(k)/sqrt(10); end JTR = 20 ; % horizontal jitter [in trials] for visibility plot(-1,-1,'ks',-1,-1,'ko',-1,1,'rs',-1,1,'bo',... % for the legend globalT(pre_tn)-JTR,g13hard(pre_tn),'rs',... globalT(pre_tf)-JTR,g13hard(pre_tf),'ro',... globalT(pre_tn)+JTR,g24hard(pre_tn),'bs',... globalT(pre_tf)+JTR,g24hard(pre_tf),'bo',... globalT(tn)-JTR,g13hard(tn),'rs-',... globalT(tn)+JTR,g24hard(tn),'bs-',... globalT(post_tn)-JTR,g13hard(post_tn),'rs',... globalT(post_tf)-JTR,g13hard(post_tf),'ro',... globalT(post_tn)+JTR,g24hard(post_tn),'bs',... globalT(post_tf)+JTR,g24hard(post_tf),'bo',... globalT(tn_opp)-JTR,g13hard(tn_opp),'ro-',... globalT(tn_opp)+JTR,g24hard(tn_opp),'bo-') ; hold on ; errorbar1(globalT-JTR,g13hard,ER1,'rn'); hold off hold on ; errorbar1(globalT+JTR,g24hard,ER2,'bn'); hold off M = 2.5 ; axis([0 N_trials 0 M]) ; grid on ; set(gca,'xtick',(0:blocks_session:N_blocks)*trials_block,'ytick',(0:ceil(M))) ; set(findobj(gca,'Color','r'),'MarkerFaceColor','r'); %set(findobj(gca,'Color','g'),'MarkerFaceColor','g'); xlabel('Trial') ; ylabel('d''') ; %title(sprintf('Group Average Pre/Post-Test, Train, and Train Opposite')); legend('Training order','Transfer order','1st order groups','2nd order groups','Location','NorthWest') ;
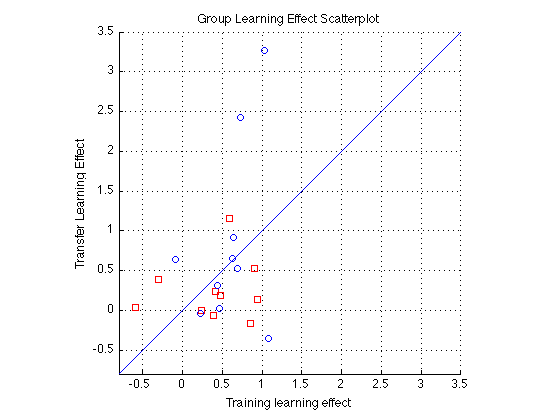
Sbj Order Learning Effect Scatter plot
pre_test = (1:4)' ; % pre-test blocks pre_tn = (3:4)' ; % pre-test training order pre_tf = (1:2)' ; % pre-test transfer order post_test = (17:20)' ; % post-test blocks post_tn = (17:18)' ; % post-test training order post_tf = (19:20)' ; % post-test transfer order tn = (3:18)' ; % train in respective order tn_opp = (19:24)' ; % train opposite order clf ; hold on ; for j=1:N_sbj LE1 = H(j).all_dprime2; base_tf = sum(LE1(pre_tf))/2; base_tn = sum(LE1(pre_tn))/2; fin_tf = sum(LE1(post_tf))/2; fin_tn = sum(LE1(post_tn))/2; % Calculate Learning effects tf_LE = (fin_tf-base_tf)/base_tf; tn_LE = (fin_tn-base_tn)/base_tn; if (gr(j)==1 || gr(j)==3) ; symb = 'rs' ; else symb = 'bo' ; end plot(tn_LE,tf_LE,symb); end hold off ; m=-.8 ; M = 3.5 ; axis([m M m M]) ; grid on ; axis square ; xlabel('Training learning effect'); ylabel('Transfer Learning Effect'); title(sprintf('Group Learning Effect Scatterplot')); refline(1,0) ;
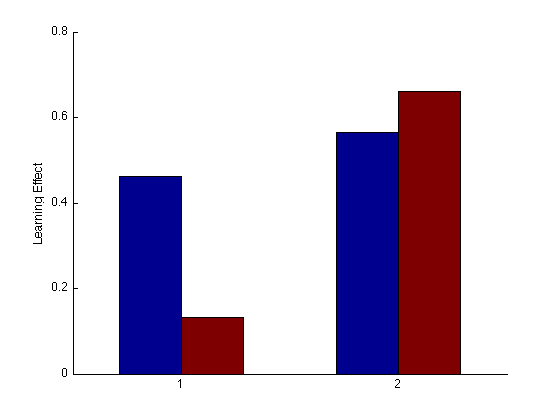
Group Order Learning Effect bar plot
%pre_tn = (3:4)' ; % pre-test training order pre_tn = (3)'; %pre_tf = (1:2)' ; % pre-test transfer order pre_tf = (1)'; post_test = (17:20)' ; % post-test blocks %post_tn = (17:18)' ; % post-test training order post_tn = (17)'; %post_tf = (19:20)' ; % post-test transfer order post_tf = (19)'; tn = (3:18)' ; % train in respective order tn_opp = (20:24)' ; % train opposite order g13 = (mdpr2(:,1)+ mdpr2(:,3))/2 ; g24 = (mdpr2(:,2) + mdpr2(:,4)) / 2 ; clf ; hold on ; base_tf1 = mean(g13(pre_tf)); base_tn1 = mean(g13(pre_tn)); fin_tf1 = mean(g13(post_tf)); fin_tn1 = mean(g13(post_tn)); % Calculate Learning effects tf_LE1 = (fin_tf1-base_tf1)/base_tf1; tn_LE1 = (fin_tn1-base_tn1)/base_tn1; base_tf2 = mean(g24(pre_tf)); base_tn2 = mean(g24(pre_tn)); fin_tf2 = mean(g24(post_tf)); fin_tn2 = mean(g24(post_tn)); % Calculate Learning effects tf_LE2 = (fin_tf2-base_tf2)/base_tf2; tn_LE2 = (fin_tn2-base_tn2)/base_tn2; hold on y = [tn_LE1 tf_LE1 tn_LE2 tf_LE2]; bar(y,1); ylabel('Learning Effect'); hold off YLIM([0 .8]); set(gca,'xtick',(0:1:4),'ytick',(0:.2:2));%'XTickLabel',{'second tn second tf','first tn first tf'}); % hold off ; % m=0 ; M = 1 ; % axis([m M m M]) ; grid on ; axis square ; % xlabel('Training learning effect'); ylabel('Transfer Learning Effect'); % title(sprintf('Group Learning Effect Scatterplot')); % refline(1,0) ;
Warning: Could not find an exact (case-sensitive) match for 'YLIM'.
/Applications/MATLAB_R2008a/toolbox/matlab/graph3d/ylim.m is a case-insensitive match and
will be used instead.
You can improve the performance of your code by using exact
name matches and we therefore recommend that you update your
usage accordingly. Alternatively, you can disable this warning using
warning('off','MATLAB:dispatcher:InexactCaseMatch').
This warning will become an error in future releases.
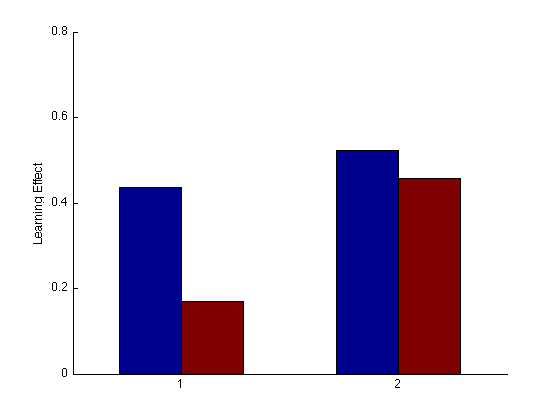
Group Order Learning Effect bar plot
pre_tn = (3:4)' ; % pre-test training order pre_tf = (1:2)' ; % pre-test transfer order post_test = (17:20)' ; % post-test blocks post_tn = (17:18)' ; % post-test training order post_tf = (19:20)' ; % post-test transfer order tn = (3:18)' ; % train in respective order tn_opp = (19:24)' ; % train opposite order g13 = (mdpr2(:,1)+ mdpr2(:,3))/2 ; g24 = (mdpr2(:,2) + mdpr2(:,4)) / 2 ; clf ; hold on ; base_tf1 = mean(g13(pre_tf)); base_tn1 = mean(g13(pre_tn)); fin_tf1 = mean(g13(post_tf)); fin_tn1 = mean(g13(post_tn)); % Calculate Learning effects tf_LE1 = (fin_tf1-base_tf1)/base_tf1; tn_LE1 = (fin_tn1-base_tn1)/base_tn1; base_tf2 = mean(g24(pre_tf)); base_tn2 = mean(g24(pre_tn)); fin_tf2 = mean(g24(post_tf)); fin_tn2 = mean(g24(post_tn)); % Calculate Learning effects tf_LE2 = (fin_tf2-base_tf2)/base_tf2; tn_LE2 = (fin_tn2-base_tn2)/base_tn2; hold on y = [tn_LE1 tf_LE1 tn_LE2 tf_LE2]; bar(y,1); ylabel('Learning Effect'); hold off YLIM([0 .8]); set(gca,'xtick',(0:1:4),'ytick',(0:.2:2));%'XTickLabel',{'second tn second tf','first tn first tf'}); % hold off ; % m=0 ; M = 1 ; % axis([m M m M]) ; grid on ; axis square ; % xlabel('Training learning effect'); ylabel('Transfer Learning Effect'); % title(sprintf('Group Learning Effect Scatterplot')); % refline(1,0) ;
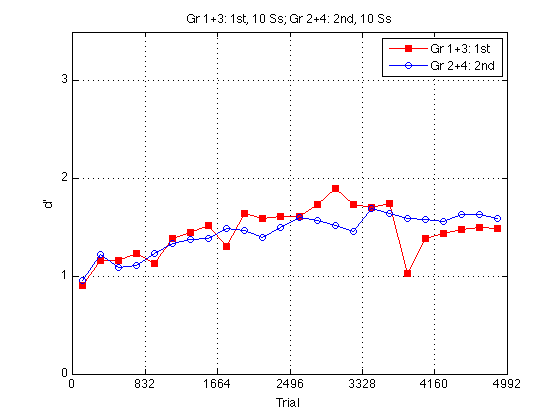
Main effect of Order on dprime:
l_1st2nd = {'Gr 1+3: 1st','Gr 2+4: 2nd'} ; % legend
Ss_1st2nd = cell(2,1) ;
for k = 1:2
if (k==1) % Train order
Ss_1st2nd{k} = find(gr==1 | gr==3) ;
else %(k==2) Train 2nd order
Ss_1st2nd{k} = find(gr==2 | gr==4) ;
end
mdpr2_1st2nd(:,k) = mean(dpr2(:,Ss_1st2nd{k}),2) ; % average over subjects
mcrit2_1st2nd(:,k) = mean(crit2(:,Ss_1st2nd{k}),2) ;
measy2_1st2nd(:,k) = mean(easy2(:,Ss_1st2nd{k}),2) ;
mhard2_1st2nd(:,k) = mean(hard2(:,Ss_1st2nd{k}),2) ;
mRT2_1st2nd(:,k) = mean(medianRT2(:,Ss_1st2nd{k}),2) ;
end
assert(isempty(intersect(Ss_1st2nd{1},Ss_1st2nd{2}))) ; % Sanity check
clf
M = 3.5 ;
plot(globalT,mdpr2_1st2nd(:,1),'rs-',...
globalT,mdpr2_1st2nd(:,2),'bo-') ;
axis([0 N_trials 0 M]) ; grid on ;
set(findobj(gca,'Color','r'),'MarkerFaceColor','r') ;
set(gca,'xtick',(0:blocks_session:N_blocks)*trials_block,'ytick',(0:ceil(M))) ;
xlabel('Trial') ; ylabel('d''') ;
title(sprintf('%s, %d Ss; %s, %d Ss',...
l_1st2nd{1},length(Ss_1st2nd{1}),l_1st2nd{2},length(Ss_1st2nd{2}))) ;
legend(l_1st2nd,'location','NorthEast') ;
Group d'prime error plot
%{ % Loop to find the mean d_prime for all subjects in block2 for k=1:N_sbj x(k) = mean(H(k).all_dprime2); end; % Loop that subtracts the mean from each point in all_dprime2 % Sets all sbj mean dprime to zero % 20 subjects x 24 adjusted dprime values for k=1:20 U(k,:) = H(k).all_dprime2(:) - x(k); end % Separate into train first and train second groups / create index gr = [H.group]; gr = gr'; idx1 = find(gr==1 | gr==3); idx2 = find(gr==2 | gr==4); U1 = U(idx1,:); U2 = U(idx2,:); % Loop to compute standard error for each block for group1 for k=1:24 E(k) = std(U1(:,k)); ER1(k) = E(k)/sqrt(10); end % Loop to compute standard error for each block for group2 for k=1:24 E(k) = std(U2(:,k)); ER2(k) = E(k)/sqrt(10); end clf M = 2.5 ; fE = errorbar(globalT-JTR,mdpr2_1st2nd(:,1),ER1.*norminv(.95),'rs-'); hold on %fE = errorbar([globalT-10;globalT+10],mdpr2_1st2nd(:),[ER1,ER2].*norminv(.95),'rs-'); sE = errorbar(globalT+JTR,mdpr2_1st2nd(:,2),ER2.*norminv(.95),'bo-'); hold off oldAx = axis; %removeErrorbarends(fE); %removeErrorbarends(sE); axis(oldAx); axis([0 N_trials 0 M]) ; grid on ; set(findobj(gca,'Color','r'),'MarkerFaceColor','r') ; set(gca,'xtick',(0:blocks_session:N_blocks)*trials_block,'ytick',(0:ceil(M))) ; %}
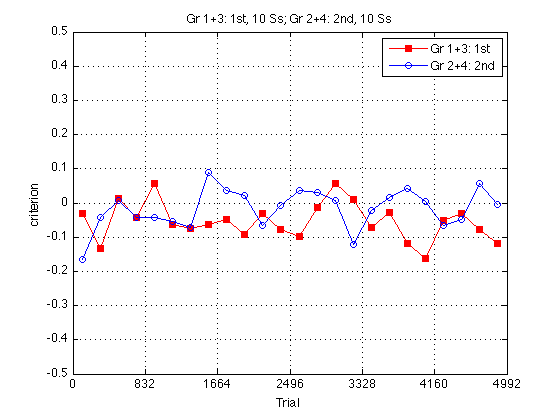
Group criterion plot:
clf m = .5 ; plot(globalT,mcrit2_1st2nd(:,1),'rs-',... globalT,mcrit2_1st2nd(:,2),'bo-') ; axis([0 N_trials -m m]) ; grid on ; set(findobj(gca,'Color','r'),'MarkerFaceColor','r') ; set(gca,'xtick',(0:blocks_session:N_blocks)*trials_block) ; xlabel('Trial') ; ylabel('criterion') ; title(sprintf('%s, %d Ss; %s, %d Ss',... l_1st2nd{1},length(Ss_1st2nd{1}),l_1st2nd{2},length(Ss_1st2nd{2}))) ; legend(l_1st2nd,'location','NorthEast') ; % sprintf('%s, %d Ss; %s, %d Ss; %s, %d Ss; %s, %d Ss',... % l{1},length(Ss{1}),l{2},length(Ss{2}),... % l{3},length(Ss{3}),l{4},length(Ss{4}))) ; % legend(l,'location','NorthWest') ; % %% Easy Delta group plot % % clf % M = 3.5 ; % plot(globalT(train1steasy),g13easy(train1steasy),'rs-',... % globalT(train2ndeasy),g24easy(train2ndeasy),'bo-') ; % axis([0 N_trials 0 M]) ; grid on ; % set(findobj(gca,'Color','r'),'MarkerFaceColor','r') ; % set(gca,'xtick',(0:blocks_session:N_blocks)*trials_block,'ytick',(0:ceil(M))) ; % xlabel('Trial') ; ylabel('d''') ; % title(sprintf('%s, %d Ss; %s, %d Ss',... % l_1st2nd{1},length(Ss_1st2nd{1}),l_1st2nd{2},length(Ss_1st2nd{2}))); % legend(l_1st2nd,'location','SouthEast') ; % % % %% Hard Delta group plot % clf % M = 3.5 ; % plot(globalT(trainhard),g13hard(trainhard),'rs--',... % globalT(trainhard),g24hard(trainhard),'bo--') % axis([0 N_trials 0 M]) ; grid on ; % set(findobj(gca,'Color','r'),'MarkerFaceColor','r') ; % set(gca,'xtick',(0:blocks_session:N_blocks)*trials_block,'ytick',(0:ceil(M))) ; % xlabel('Trial') ; ylabel('d''') ; % title(sprintf('%s, %d Ss; %s, %d Ss',... % l_1st2nd{1},length(Ss_1st2nd{1}),l_1st2nd{2},length(Ss_1st2nd{2}))); % legend(l_1st2nd,'location','SouthEast') ;
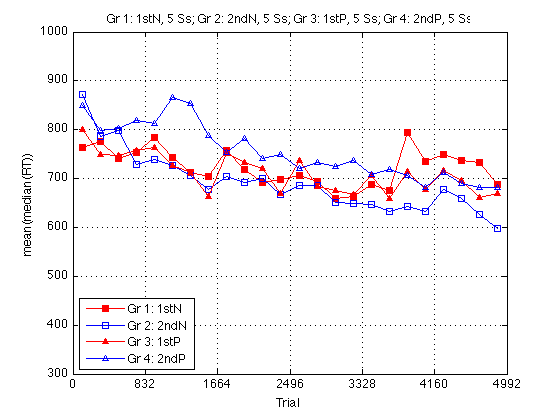
Group RT plot
clf M = 1000 ; % msec m = 300 ; plot(globalT,mRT2(:,1),'rs-',... globalT,mRT2(:,2),'bs-',... globalT,mRT2(:,3),'r^-',... globalT,mRT2(:,4),'b^-') ; axis([0 N_trials m M]) ; grid on ; set(findobj(gca,'Color','r'),'MarkerFaceColor','r') ; set(gca,'xtick',(0:blocks_session:N_blocks)*trials_block) ; xlabel('Trial') ; ylabel('mean(median(RT))') ; title(sprintf('%s, %d Ss; %s, %d Ss; %s, %d Ss; %s, %d Ss',... l{1},length(Ss{1}),l{2},length(Ss{2}),... l{3},length(Ss{3}),l{4},length(Ss{4}))) ; legend(l,'location','SouthWest') ; % %% Plot all RT Distributions % sbj = 25; % clf; hold on; % for k =1:sbj % subplot(5,5,k); % x = D(1,k).data(:,15); % idx = find(x<4000); % RT = x(idx,:); % hist(RT,50); % axis([0 3500 0 2000]); % xlabel('time ms', 'fontsize', 8); % %set(gca,'fontsize',14); % end % %% Individual RT Plot % % for individual plots replace k with value 1-25 % x = D(1,5).data(:,15); % idx = find(x<4000); % RT = x(idx,:); % hist(RT,90); % axis([0 3000 0 1000]); % h = findobj(gca,'Type','patch'); % set(h,'FaceColor','b','EdgeColor','w'); % xlabel('time ms', 'fontsize', 16); ylabel('frequency','fontsize',16); % title('Sbj 132','fontsize',18); % set(gca,'fontsize',14);
Main effect of Order on RT
clf M = 1100 ; % msec m = 500 ; plot(globalT,mRT2_1st2nd(:,1),'rs-',... globalT,mRT2_1st2nd(:,2),'bo-') ; axis([0 N_trials m M]) ; grid on ; set(findobj(gca,'Color','r'),'MarkerFaceColor','r') ; set(gca,'xtick',(0:blocks_session:N_blocks)*trials_block) ; xlabel('Trial') ; ylabel('mean(median(RT))') ; title(sprintf('%s, %d Ss; %s, %d Ss',... l_1st2nd{1},length(Ss_1st2nd{1}),l_1st2nd{2},length(Ss_1st2nd{2}))) ; legend(l_1st2nd,'location','NorthEast') ;
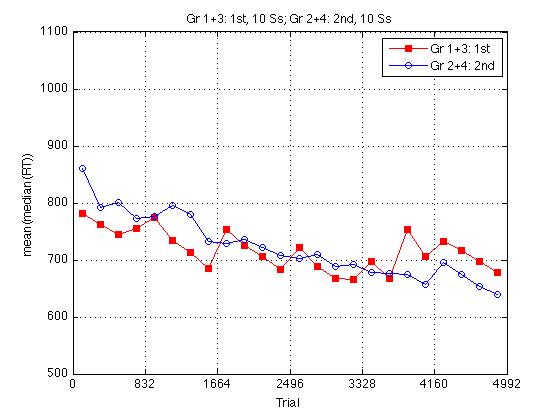
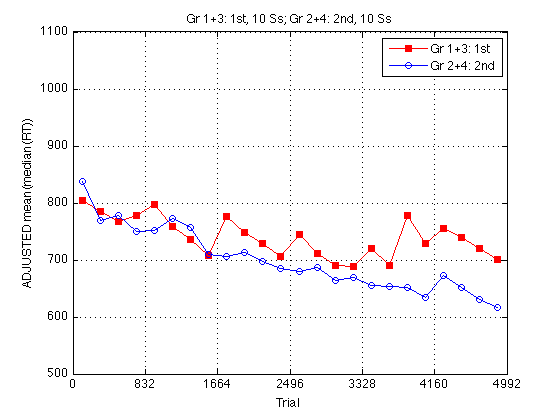
Adjusted group RT plot
Adjust all RTs so that the two curves have the same mean on the pretest, which is identical for both groups.
clf baseRT1 = mean(mRT2_1st2nd(pre_test,1)) ; baseRT2 = mean(mRT2_1st2nd(pre_test,2)) ; baseRT_adjustment = [baseRT2-baseRT1 , baseRT1-baseRT2] ./ 2 ; fprintf('\nMean RT(Gr1+3,day1)=%.0f, Mean RT(Gr2+4,day1)=%.0f, adjustment=2*%.0f msec.\n',... baseRT1,baseRT2,baseRT_adjustment(1)) ; mRT2_1st2nd_adj = mRT2_1st2nd + repmat(baseRT_adjustment,size(mRT2_1st2nd,1),1) ; plot(globalT,mRT2_1st2nd_adj(:,1),'rs-',... globalT,mRT2_1st2nd_adj(:,2),'bo-') ; axis([0 N_trials m M]) ; grid on ; set(findobj(gca,'Color','r'),'MarkerFaceColor','r') ; set(gca,'xtick',(0:blocks_session:N_blocks)*trials_block) ; xlabel('Trial') ; ylabel('ADJUSTED mean(median(RT))') ; title(sprintf('%s, %d Ss; %s, %d Ss',... l_1st2nd{1},length(Ss_1st2nd{1}),l_1st2nd{2},length(Ss_1st2nd{2}))) ; legend(l_1st2nd,'location','NorthEast') ;
Mean RT(Gr1+3,day1)=761, Mean RT(Gr2+4,day1)=807, adjustment=2*23 msec.