Contents
- 010: Get some data. In this script, we use data from LRaven1 experiment.
- 020: Load H and the sequence data
- 030: Define constants
- 040: Define score targets based on cond and session info
- 050: Define Constants that vary based on cond and session
- 060: Calculate successor rep for each sequence, with default params
- 070: Average the SR matrices across trials:
- 080: Convert the 10x10 matrix to 1x100 row vector
- 090: Center the mean of each SR cell across Ss
- 095: Does it help to divide by the std.deviation of each cell?
- 100: Principal Component Analysis using Shlens' conventions
- 110: Plot a tableau of all matrices involved
- 120: Archive these matrices and clear them from the workspace
- 130: Transpose the data so that variables (or "dimensions") are columns
- 140: Plot a tableau of all matrices involved
- 150: Archive these matrices and clear them from the workspace
- 160: Verify the equivalence
- 170: Run SVD in economy mode
- 180: Plot a tableau of all matrices involved
- 190: Archive these matrices. Do not clear them from the workspace
- 200: Verify that economy mode returns a subset of what the full mode returns
- 210: Multiple regression
- 220: Correlate each component with the target score
- 230: Select the top NC components with highest delta_R2
- 240: Re-run the regression on the best components
- 250: Define a benchmark data set
- 260: Calculate weights that can predict scores for arbitrary data
- 270: Visualize W1 as a matrix
- 280: Predict benchmark scores using W
- 290: Verify that weight_based_yhat == benchmark_yhat
- 300: Visualize M_35x100_mean as a matrix
- 310: Visualize M_35x100_std as a matrix
- 320: Cross-validated R-square
- 330: Sanity check: Scramble the scores and cross-validate again
- 340: Prepare to call LRaven1_R2_goalfun.m
- 350: Verify that LRaven1_R2_goalfun reproduces the components
- 360: Are the Borda components the same as the globally selected ones?
- 999: Finish
% LR1_SVD_study.m % % A study in singular-value decomposition (SVD) in service of prediction. % What matrix should be used to convert the raw scores of new cases that % have not been part of the original SVD call? % % File: work/RelExper/LRaven1/matlab/etc/LR1_SVD_study.m % Usage: publish('LR1_SVD_study.m','html') ; % 'latex','doc','ppt' % % Reference: Great tutorial on PCA and SVD available on-line: % Shlens, J. (2009) A Tutorial on Principal Component Analysis. % http://www.snl.salk.edu/~shlens/ % % (c) Laboratory for Cognitive Modeling and Computational Cognitive % Neuroscience at the Ohio State University, http://cogmod.osu.edu % % 1.0.2 2011-01-25 AAP: Scatterplot in Sect.280. LR1_R2_goalfun returns cvRMSE % Ignore M_35x100_std when visualizing W in Sect.270. % 1.0.1 2011-01-15 AAP: Swap var_idx and case_idx args to regress_subset % Added cross-validation section 320 % Test cross-LRaven1_R2_goalfun.m in section 350 % 1.0.0 2011-01-14 AAP: Initial version, based on LRaven1_successor_plot.m
010: Get some data. In this script, we use data from LRaven1 experiment.
cd(fullfile(LRaven1_pathstr,'etc')) ; fprintf('\n\nLR1_SVD_study executed on %s.\n\n',datestr(now)) ; fprintf('cd %s\n',pwd) ; clear all ; close all ;
LR1_SVD_study executed on 25-Jan-2011 19:17:11. cd /Users/apetrov/a/r/w/work/RelExper/LRaven1/matlab/etc
020: Load H and the sequence data
% Load H filename = fullfile(LRaven1_pathstr,'data','H.mat') ; load(filename) ; % Load temporal bin sequence data trans_pathstr = fullfile(LRaven1_pathstr,'data','transitions') ; filename = fullfile(trans_pathstr,'final_sequence.mat') ; load(filename) ; clearvars -except params H recoded_sequences
030: Define constants
params.gamma = 0.3 ; params.lambda_gamma = 0.2 ; params.lrate = 0.1 ; % AOI and component number N_AOIs = 10 ; % Areas of Interest (AOIs) Tick=1:N_AOIs; TickLabel='1|2|3|4|5|6|7|8|9|R'; % Interpretation of the 10 AOIs NC = 3 ; % Number of "best" components used in final regression max_NC = 12 ; % Max number of components, from which NC "best" are selected TOL = 1e-8 ; % tolerance for equality assertions
040: Define score targets based on cond and session info
% Slice these main score sets to get other options omni_score_both = [H.session1_score]' + [H.session2_score]' ; % [N_sbj 1] omni_score_s1 = [H.session1_score]' ; omni_score_s2 = [H.session2_score]' ;
050: Define Constants that vary based on cond and session
N_sbj = size(recoded_sequences,1) ; % number of subjects assert(size(recoded_sequences,1)==N_sbj) ; N_trials = size(recoded_sequences,2) ; % number of trials assert(size(recoded_sequences,2)==N_trials) ;
060: Calculate successor rep for each sequence, with default params
M_by_sbj_by_trial = NaN([N_sbj,N_trials, N_AOIs N_AOIs]) ; for s = 1:N_sbj for k = 1:N_trials %- isolate the sequence seq = recoded_sequences{s,k} ; %- Calculate and store the successor representation % (If length(seq)==1, the result is a matrix of zeros.) M_by_sbj_by_trial(s,k,:,:) = successrep_learn(seq,N_AOIs,params) ; %-- Debug: % if (any(isnan(M(:)))) % fprintf('s=%2d, k=%2d, gamma=%.6f, lrate=%.6f, l_g=%.6f returns NaN(s)\n',... % s, k, params.gamma, params.lrate, params.lambda_gamma) ; % end end end clearvars s k seq
070: Average the SR matrices across trials:
M_by_sbj = squeeze(mean(M_by_sbj_by_trial,2)) ; % [N_sbj N_AOIs N_AOIs]
080: Convert the 10x10 matrix to 1x100 row vector
N_vars = N_AOIs*N_AOIs ; M_35x100 = reshape(M_by_sbj,N_sbj,N_vars) ;
090: Center the mean of each SR cell across Ss
[zM_35x100,M_35x100_mean,M_35x100_std] = zscore(M_35x100) ;
M_35x100_mean = mean(M_35x100) ; % [1 x N_vars] zM_35x100 = bsxfun(@minus,M_35x100,M_35x100_mean) ; % zero mean
095: Does it help to divide by the std.deviation of each cell?
%divide_std_dev_p = false ; % not recommended, see Sect.270 divide_std_dev_p = true ; % recommended because yields more interpretable weights if (divide_std_dev_p) M_35x100_std = std(M_35x100) ; % [1 x N_vars] zM_35x100 = bsxfun(@rdivide,zM_35x100,M_35x100_std) ; % unit std.dev %else leave zM_35x100 alone end % zM_35x100 is the raw data matrix [N_subjects, N_vars] as far as SVD is concerned.
100: Principal Component Analysis using Shlens' conventions
% Compute components using SVD % Numerically, PCA is an SVD of a centered data matrix % % In Shlens' tutorial, this is referred to as the "second method" described % in Section VI and implemented in Matlab function pca2.m in Appendix B. %- Step 0: Convert our matrix zM_35x100 to Shlens' conventions: % * rows = "dimensions" = variables in our terminology % N_vars = 100 % * columns = "cases" = subjects in our terminology % N_sbj = 35 data = zM_35x100' ; % [N_vars, N_sbj] assert(size(data,1)==N_vars) ; assert(size(data,2)==N_sbj) ; %- Step 1: Centering -- already done for zM_35x100 in Section 090 above %- Step 2: Construct the matrix Y % Note that data is transposed again and thus size(Y)==size(zM_35x100) Y = data' ./ sqrt(N_sbj-1) ; % Equation on top of page 9, left column %- Step 3: Call SVD to decompose Y: Y==U*Sigma*PC' % Full mode (as opposed to economical mode) [U,Sigma,PC] = svd(Y) ; %- Verify the identity that defines SVD: Y == U*Sigma*PC' Y_hat = U*Sigma*PC' ; assert(max(abs(Y(:)-Y_hat(:)))<TOL) ; clearvars Y_hat %- Step 4: Calculate the variance for each PC % Note that var_PC(end)==0 (within rounding error) because we lost one % degree of freedom in the centering in Step 1 above. var_PC = diag(Sigma).^2 ; % [N_vars x 1] assert(abs(var_PC(end))<TOL) ; %- Step 5: Project the original data onto the orthogonal coordinate axes % defined by the principal components. The result is a matrix of % "signals" of the same dimension as the input data matrix: % * rows = "dimensions" = variables in our terminology % N_vars = 100 % * columns = "cases" = subjects in our terminology % N_sbj = 35 signals = PC' * data ; assert(all(size(signals)==size(data))) ; % Note that the bottom rows (N_sbj:N_vars) are zeros (within rounding err). % This assumes that N_sbj<N_vars. Not sure what happens when N_sbj>N_vars. foo = signals(N_sbj:N_vars,:) ; assert(max(abs(foo(:)))<TOL) ; clearvars foo
110: Plot a tableau of all matrices involved
Compare with Fig.4 in ShlensJ09.pdf
subplot(2,3,1) ; foo = data ; imagesc(abs(foo)) ; title(sprintf('data [%d x %d]',size(foo,1),size(foo,2))) ; subplot(2,3,2) ; foo = Y ; imagesc(abs(foo)) ; title(sprintf('Y [%d x %d]',size(foo,1),size(foo,2))) ; subplot(2,3,3) ; foo = signals ; imagesc(abs(foo)) ; title(sprintf('signals [%d x %d]',size(foo,1),size(foo,2))) ; subplot(2,3,4) ; foo = U ; imagesc(abs(foo)) ; title(sprintf('U [%d x %d]',size(foo,1),size(foo,2))) ; subplot(2,3,5) ; foo = Sigma ; imagesc(foo) ; title(sprintf('Sigma [%d x %d]',size(foo,1),size(foo,2))) ; subplot(2,3,6) ; foo = PC ; imagesc(abs(foo)) ; title(sprintf('PC [%d x %d], aka V',size(foo,1),size(foo,2))) ; clear foo

120: Archive these matrices and clear them from the workspace
full_mode_Shlens_layout.data = data ; full_mode_Shlens_layout.Y = Y ; full_mode_Shlens_layout.U = U ; full_mode_Shlens_layout.Sigma = Sigma ; full_mode_Shlens_layout.PC = PC ; full_mode_Shlens_layout.signals = signals %#ok<NOPTS> clearvars data Y U Sigma PC signals
full_mode_Shlens_layout =
data: [100x35 double]
Y: [35x100 double]
U: [35x35 double]
Sigma: [35x100 double]
PC: [100x100 double]
signals: [100x35 double]
130: Transpose the data so that variables (or "dimensions") are columns
Matlab's native format (and the format adopted for M_35x100) is: * rows = "cases" = subjects in our terminology % N_sbj = 35 * columns = "dimensions" = variables in our terminology % N_vars = 100
Also, let's rename the variable "signals" to "projections".
Re-implement Shlens "second method", making the necessary transpositions:
%- Step 0: Our matrix zM_35x100 follows the Matlab convention: % * rows = "cases" = subjects in our terminology % N_sbj = 35 % * columns = "dimensions" = variables in our terminology % N_vars = 100 data = zM_35x100 ; % [N_sbj, N_vars] assert(size(data,1)==N_sbj) ; assert(size(data,2)==N_vars) ; %- Step 1: Centering -- already done for zM_35x100 in Section 090 above % Note that Shens' algorithm used row-wise means: mn=mean(data,2) % Thus, when we transpose data, we end up with the default column-wise % means which are implemented in the zscore call above %- Step 2: Construct the matrix Y % Now we do *not* transpose. Thus size(Y)==size(zM_35x100) is still true: Y = data ./ sqrt(N_sbj-1) ; % Equation on top of page 9, left column %- Step 3: Call SVD to decompose Y: Y==U*Sigma*PC' % Full mode (as opposed to economical mode) [U,Sigma,PC] = svd(Y) ; %- Verify the identity that defines SVD: Y == U*Sigma*PC' Y_hat = U*Sigma*PC' ; assert(max(abs(Y(:)-Y_hat(:)))<TOL) ; clearvars Y_hat %- Step 4: Calculate the variance for each PC % Note that var_PC(end)==0 (within rounding error) because we lost one % degree of freedom in the centering in Step 1 above. var_PC = diag(Sigma).^2 ; % [N_vars x 1] assert(abs(var_PC(end))<TOL) ; %- Step 5: Project the original data onto the orthogonal coordinate axes % defined by the principal components. The result is a matrix of % "projections" of the same dimension as the input data matrix: % * rows = "cases" = subjects in our terminology % N_sbj = 35 % * columns = "dimensions" = variables in our terminology % N_vars = 100 projections = data * PC ; assert(all(size(projections)==size(data))) ; % Now the rightmost columns (N_sbj:N_vars) are zeros (within rounding err). % This assumes that N_sbj<N_vars. Not sure what happens when N_sbj>N_vars. foo = projections(:,N_sbj:N_vars) ; % [35x66] assert(max(abs(foo(:)))<TOL) ; clearvars foo
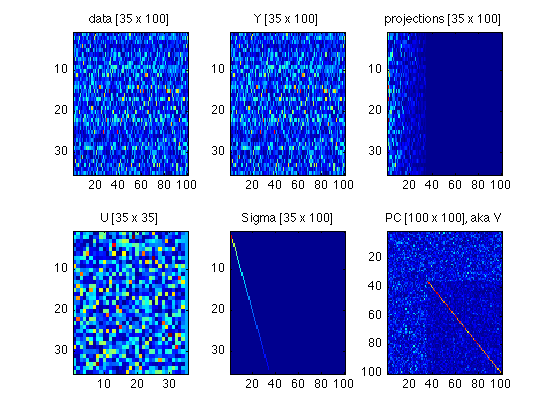
140: Plot a tableau of all matrices involved
Compare with Fig.4 in ShlensJ09.pdf
subplot(2,3,1) ; foo = data ; imagesc(abs(foo)) ; title(sprintf('data [%d x %d]',size(foo,1),size(foo,2))) ; subplot(2,3,2) ; foo = Y ; imagesc(abs(foo)) ; title(sprintf('Y [%d x %d]',size(foo,1),size(foo,2))) ; subplot(2,3,3) ; foo = projections ; imagesc(abs(foo)) ; title(sprintf('projections [%d x %d]',size(foo,1),size(foo,2))) ; subplot(2,3,4) ; foo = U ; imagesc(abs(foo)) ; title(sprintf('U [%d x %d]',size(foo,1),size(foo,2))) ; subplot(2,3,5) ; foo = Sigma ; imagesc(foo) ; title(sprintf('Sigma [%d x %d]',size(foo,1),size(foo,2))) ; subplot(2,3,6) ; foo = PC ; imagesc(abs(foo)) ; title(sprintf('PC [%d x %d], aka V',size(foo,1),size(foo,2))) ; clear foo
150: Archive these matrices and clear them from the workspace
full_mode.data = data ; full_mode.Y = Y ; full_mode.U = U ; full_mode.Sigma = Sigma ; full_mode.PC = PC ; full_mode.projections = projections %#ok<NOPTS> clearvars data Y U Sigma PC projections
full_mode =
data: [35x100 double]
Y: [35x100 double]
U: [35x35 double]
Sigma: [35x100 double]
PC: [100x100 double]
projections: [35x100 double]
160: Verify the equivalence
delta = full_mode.data - full_mode_Shlens_layout.data' ; % transposed assert(max(abs(delta(:)))<TOL) ; delta = full_mode.PC - full_mode_Shlens_layout.PC ; % NOT transposed assert(max(abs(delta(:)))<TOL) ; delta = full_mode.projections - full_mode_Shlens_layout.signals' ; % transposed assert(max(abs(delta(:)))<TOL) ; clearvars delta
170: Run SVD in economy mode
We don't need more components than the rank of the data matrix (minus 1). Thus, there is no need for SVD to calculate their coefficients, given that the relevant entries in the Sigma matrix will be zeros. The code below has been tested assuming N_sbj < N_vars (35<100 in our case).
WARNING: Things may break when N_sbj >= N_vars. It is up to you to do the necessary tests (and, possibly, adjustments) if you need to analyze data with more cases than variables.
%- Step 0: Our matrix zM_35x100 follows the Matlab convention: % * rows = "cases" = subjects in our terminology % N_sbj = 35 % * columns = "dimensions" = variables in our terminology % N_vars = 100 data = zM_35x100 ; % [N_sbj, N_vars] assert(size(data,1)==N_sbj) ; assert(size(data,2)==N_vars) ; %- Step 1: Centering -- already done for zM_35x100 in Section 090 above % Note that Shens' algorithm used row-wise means: mn=mean(data,2) % Thus, when we transpose data, we end up with the default column-wise % means which are implemented in the zscore call above %- Step 2: Construct the matrix Y % Now we do *not* transpose. Thus size(Y)==size(zM_35x100) is still true: Y = data ./ sqrt(N_sbj-1) ; % Equation on top of page 9, left column %- Step 3: Call SVD to decompose Y: Y==U*Sigma*PC' % ECONOMY mode (as opposed to full mode) [U,Sigma,PC] = svd(Y,'econ') ; % The identity that defines SVD still holds: Y == U*Sigma*PC' Y_hat = U*Sigma*PC' ; assert(max(abs(Y(:)-Y_hat(:)))<TOL) ; clearvars Y_hat %- Step 4: Calculate the variance for each PC % Note that var_PC(end)==0 (within rounding error) because we lost one % degree of freedom in the centering in Step 1 above. var_PC = diag(Sigma).^2 ; % [N_vars x 1] assert(abs(var_PC(end))<TOL) ; % - Step 5: Project the original data onto the orthogonal coordinate axes % defined by the principal components. The result is a matrix of % "projections" of the same dimension as the input data matrix: % * rows = "cases" = subjects in our terminology % N_sbj = 35 % * columns = "dimensions" = variables in our terminology % truncated! projections = data * PC ; % [35 x 35] now rather than [35 x 100] % It no longer holds that size(projections)==size(data) % But the rightmost projections were useless anyway. We still have the % low-numbered PCs, which are what we need for regressions and such.
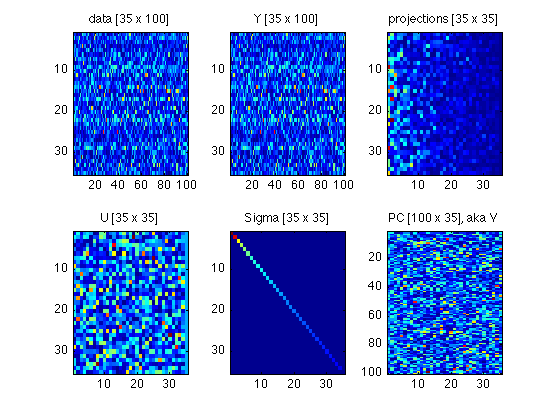
180: Plot a tableau of all matrices involved
Compare with Fig.4 in ShlensJ09.pdf
subplot(2,3,1) ; foo = data ; imagesc(abs(foo)) ; title(sprintf('data [%d x %d]',size(foo,1),size(foo,2))) ; subplot(2,3,2) ; foo = Y ; imagesc(abs(foo)) ; title(sprintf('Y [%d x %d]',size(foo,1),size(foo,2))) ; subplot(2,3,3) ; foo = projections ; imagesc(abs(foo)) ; title(sprintf('projections [%d x %d]',size(foo,1),size(foo,2))) ; subplot(2,3,4) ; foo = U ; imagesc(abs(foo)) ; title(sprintf('U [%d x %d]',size(foo,1),size(foo,2))) ; subplot(2,3,5) ; foo = Sigma ; imagesc(foo) ; title(sprintf('Sigma [%d x %d]',size(foo,1),size(foo,2))) ; subplot(2,3,6) ; foo = PC ; imagesc(abs(foo)) ; title(sprintf('PC [%d x %d], aka V',size(foo,1),size(foo,2))) ; clear foo
190: Archive these matrices. Do not clear them from the workspace
econ_mode.data = data ;
econ_mode.Y = Y ;
econ_mode.U = U ;
econ_mode.Sigma = Sigma ;
econ_mode.PC = PC ;
econ_mode.projections = projections %#ok<NOPTS>
econ_mode =
data: [35x100 double]
Y: [35x100 double]
U: [35x35 double]
Sigma: [35x35 double]
PC: [100x35 double]
projections: [35x35 double]
200: Verify that economy mode returns a subset of what the full mode returns
Again, all this assumes that N_sbj<N_vars. It will not work otherwise.
delta = full_mode.U - econ_mode.U ; % both are [N_sbj x N_sbj] assert(max(abs(delta(:)))<TOL) ; delta = full_mode.Sigma(:,1:N_sbj) - econ_mode.Sigma ; assert(max(abs(delta(:)))<TOL) ; delta = full_mode.PC(:,1:N_sbj) - econ_mode.PC ; assert(max(abs(delta(:)))<TOL) ; delta = full_mode.projections(:,1:N_sbj) - econ_mode.projections ; assert(max(abs(delta(:)))<TOL) ; clearvars delta
210: Multiple regression
Predict omni_score_both using the first max_NC projections
var_idx = (1:max_NC) ; case_idx = (1:N_sbj)' ; % do all subjects in this example, leave nobody out reg12 = regress_subset(omni_score_both,projections,case_idx,var_idx) %#ok<NOPTS>
reg12 =
y: [35x1 double]
X: [35x35 double]
var_idx: [1 2 3 4 5 6 7 8 9 10 11 12]
case_idx: [35x1 double]
X1: [35x13 double]
beta: [1x13 double]
R2: 0.6150
yhat: [35x1 double]
220: Correlate each component with the target score
The function utils/regression/select_components_Borda.m is based on this:
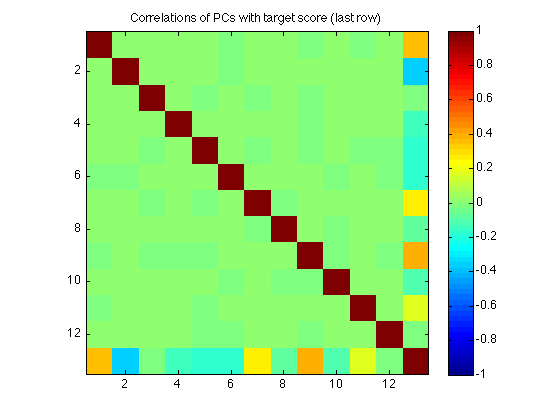
C = corrcoef([projections(:,var_idx) , omni_score_both]) ; % [max_NC+1 x max_NC+1] % Because the PCs form an orthonormal basis, the correlation matrix C is % the identity matrix: clf imagesc(C,[-1 1]) ; axis square ; colorbar ; title('Correlations of PCs with target score (last row)') ; % The last row (and column) gives the correlation with the target score. % As the PCs do not share variance, the *multiple* correlation R2 of a % regression model using any subset of components simply equals the sum % of the squared correlations with each individual component in the set % and the target score: diff_R2 = C(end,1:length(var_idx)).^2 %#ok<NOPTS> calculated_R2 = sum(diff_R2(var_idx)) %#ok<NOPTS> assert(max(abs(reg12.R2-calculated_R2))<TOL) ; clearvars C calculated_R2
diff_R2 =
Columns 1 through 11
0.1402 0.1278 0.0000 0.0159 0.0268 0.0320 0.0773 0.0059 0.1495 0.0140 0.0256
Column 12
0.0000
calculated_R2 =
0.6150
230: Select the top NC components with highest delta_R2
[ignore,idx] = sort(diff_R2,'descend') ; best_comp = idx(1:NC) %#ok<NOPTS>
best_comp =
9 1 2
240: Re-run the regression on the best components
Note that this isn't really necessary -- the beta coefficients will be the same (again, because the PCs are orthogonal and don't share variance). Still, it is computationally cheap and implementaitonally easier just to re-run regress_subset on the best_comp index. It is also a safeguard against inconsistencies introduced by future changes in the code.
reg3 = regress_subset(omni_score_both,projections,case_idx,best_comp) %#ok<NOPTS> calculated_R2 = sum(diff_R2(best_comp)) ; assert(max(abs(reg3.R2-calculated_R2))<TOL) ; clearvars calculated_R2
reg3 =
y: [35x1 double]
X: [35x35 double]
var_idx: [9 1 2]
case_idx: [35x1 double]
X1: [35x4 double]
beta: [0.8171 0.3063 -0.3280 21.9429]
R2: 0.4176
yhat: [35x1 double]
250: Define a benchmark data set
Suppose a new subject comes in, one whose successor rep was not part of the SVD call that defined the components. We want to be able to predict the Raven score for such new subject(s). To that end, we stack all the linear transformations into a single weight vector and a single additive constant term.
To help wrap our heads around this, let's recapitulate the steps. We'll do it on new_M that just happens to be a random permutation of the original M.
old2new_mapping = randperm(N_sbj) ; new_M = M_35x100(old2new_mapping,:) ; benchmark_yhat = reg3.yhat(old2new_mapping) ;
260: Calculate weights that can predict scores for arbitrary data
We will work backwards, beginning with the last step and going up: 1. yhat = projections(:,best_comp) * beta(1:NC)' + beta(NC+1) 2. projections(:,best_comp) = data * PC(:,best_comp) ; 3. yhat = (data * PC(:,best_comp)) * beta(1:NC)' + beta(NC+1) 4. data = zscore(M) = (M-mean_M)./std_M 5. yhat = (((M-mean_M)./std_M) * PC(:,best_comp)) * beta(1:NC)' + beta(NC+1) 6. (M./s) * P = M * (P./s) 7. yhat = ((M-mean_M) * (PC(:,best_comp)./std_M)) * beta(1:NC)' + beta(NC+1) 8. Let Z:=(PC(:,best_comp)./std_M)) ; b:=beta(1:NC)' ; c1:=beta(NC+1) 9. yhat = (M-mean_M)*Z*b + c1
%10. yhat = M*Z*b - mean_M*Z*b + c1 = M*Z*b + (c1-mean_M*Z*b) %11. Weights W = Z*b = (PC(:,best_comp)./std_M)) * beta(1:NC)' %12. Alternatively: W = (PC(:,best_comp)*beta(1:NC)') ./std_M %13. additive_const = beta(NC+1) - W*mean_M % Calculate weight vector W [= weight_matrix(:)] defined in 12. above: % Note that this combines the NC components into a single weight vector. W = PC(:,best_comp) * reg3.beta(1:NC)' ; % [N_vars x NC] * [NC x 1] = [N_vars x 1] W1 = W ; % for plotting in Sect. 270 below if (divide_std_dev_p) W = W ./ M_35x100_std' ; %else leave W alone end % Additive constant from step 12. above const_term = reg3.beta(end) - M_35x100_mean * W %#ok<NOPTS>
const_term = 15.3969
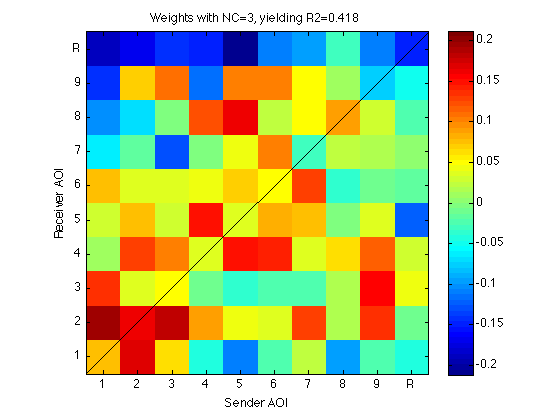
270: Visualize W1 as a matrix
clf mmm = 0.8*max(abs(W1(:))) ; imagesc(reshape(W1,N_AOIs,N_AOIs),[-mmm mmm]); title(sprintf('Weights with NC=%d, yielding R2=%.3f',NC,reg3.R2)) ; axis xy;axis square;colorbar ; h=refline(1,0);set(h,'Color','k'); clear h set(gca,'XTick',Tick,'XTickLabel',TickLabel,'YTick',Tick,'YTickLabel',TickLabel); xlabel('Sender AOI'); ylabel('Receiver AOI'); clearvars mmm
280: Predict benchmark scores using W
weight_based_yhat = new_M * W + const_term ; % [size(new_M,1) x 1] clf plot(omni_score_both,weight_based_yhat,'o') ; xlabel('Observed score') ; ylabel('Predicted score') ; grid on
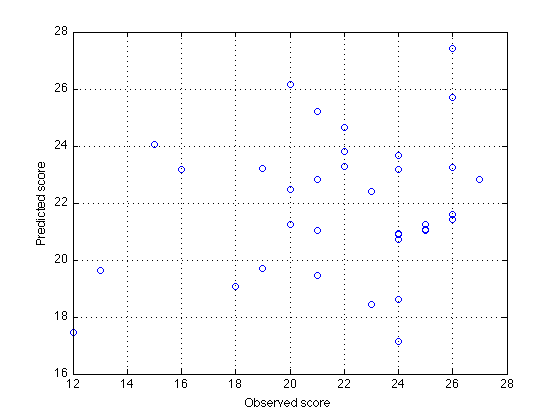
290: Verify that weight_based_yhat == benchmark_yhat
discrepancy = weight_based_yhat - benchmark_yhat ; describe(discrepancy) assert(max(abs(discrepancy))<TOL) ;
Mean Std.dev Min Q25 Median Q75 Max
------------------------------------------------------------
-0.000 0.000 -0.00 -0.00 0.00 0.00 0.00
300: Visualize M_35x100_mean as a matrix
clf mmm = 0.5*max(abs(M_35x100_mean(:))) ; imagesc(reshape(M_35x100_mean,N_AOIs,N_AOIs),[0 mmm]); title(sprintf('Mean of each SR cell (across %d subjects)',N_sbj)) ; axis xy;axis square;colorbar ; h=refline(1,0);set(h,'Color','k'); clear h set(gca,'XTick',Tick,'XTickLabel',TickLabel,'YTick',Tick,'YTickLabel',TickLabel); xlabel('Sender AOI'); ylabel('Receiver AOI'); clearvars mmm
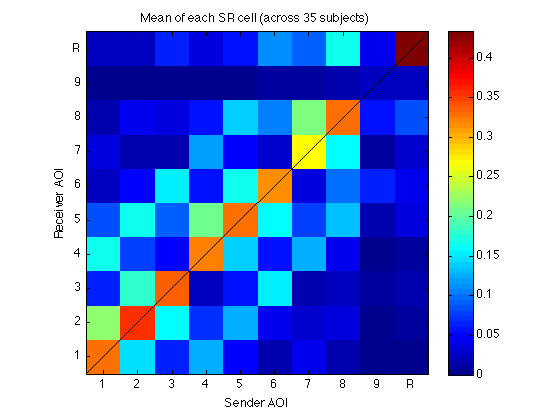
310: Visualize M_35x100_std as a matrix
if (divide_std_dev_p) clf mmm = 0.8*max(abs(M_35x100_std(:))) ; imagesc(reshape(M_35x100_std,N_AOIs,N_AOIs),[0 mmm]); title(sprintf('Std.dev of each SR cell (across %d subjects)',N_sbj)) ; axis xy;axis square;colorbar ; h=refline(1,0);set(h,'Color','k'); clear h set(gca,'XTick',Tick,'XTickLabel',TickLabel,'YTick',Tick,'YTickLabel',TickLabel); xlabel('Sender AOI'); ylabel('Receiver AOI'); clearvars mmm %else do nothing: M_35x100_std is just a vector of 1s end
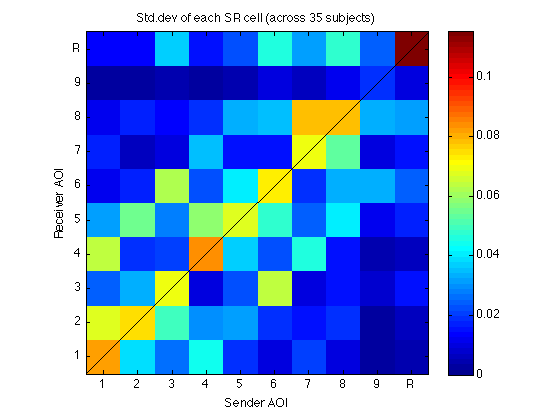
320: Cross-validated R-square
Let's use (and test) the newly defined utils/regress/cross_validated_R2.m. We will do a leave-TWO-out cross validation, 595 (=35*34/2) sets in total.
N_left_out = 2 ; % leave two cases (=subjects) from each set case_sets = nchoosek(1:N_sbj,N_sbj-N_left_out) ; cvR = cross_validated_R2(omni_score_both,projections,case_sets,best_comp) %#ok<NOPTS> describe(cvR.R2_set)
cvR =
y: [35x1 double]
X: [35x35 double]
case_sets: [595x33 double]
beta: [595x4 double]
R2_set: [595x1 double]
y_train: [595x33 double]
y_test: [595x2 double]
yhat_train: [595x33 double]
yhat_test: [595x2 double]
R2_train: 0.4230
R2_test: 0.2427
RMSE_train: 2.8067
RMSE_test: 3.2769
Mean Std.dev Min Q25 Median Q75 Max
------------------------------------------------------------
0.421 0.037 0.29 0.41 0.42 0.44 0.54
330: Sanity check: Scramble the scores and cross-validate again
scramble_idx = randperm(N_sbj) ; cvR_scrambled = cross_validated_R2(omni_score_both(scramble_idx),... projections,case_sets,best_comp) %#ok<NOPTS> describe(cvR_scrambled.R2_set)
cvR_scrambled =
y: [35x1 double]
X: [35x35 double]
case_sets: [595x33 double]
beta: [595x4 double]
R2_set: [595x1 double]
y_train: [595x33 double]
y_test: [595x2 double]
yhat_train: [595x33 double]
yhat_test: [595x2 double]
R2_train: 0.2245
R2_test: 0.0473
RMSE_train: 3.2540
RMSE_test: 3.7166
Mean Std.dev Min Q25 Median Q75 Max
------------------------------------------------------------
0.224 0.048 0.09 0.20 0.22 0.24 0.44
340: Prepare to call LRaven1_R2_goalfun.m
This is a test of ../prog/LRaven1_R2_goalfun.m, which was developed on the basis of the current script.
%- Prepare the structure D, which holds the original fixation sequences D.sequences = recoded_sequences ; D.target = omni_score_both ; %- Prepare search_params search_params.N_AOIs = N_AOIs ; search_params.N_comp = NC ; search_params.max_N_comp = max_NC ; search_params.sbj_idx = (1:N_sbj) ; % that is, all subjects search_params.trial_idx = (1:N_trials) ; % all trials search_params.N_left_out = N_left_out ; search_params.Borda_diagnosep = true %#ok<NOPTS> %- To avoid recalculating the SRs, add them to D: D.SR_params = params ; D.trial_idx = search_params.trial_idx ; D.SR_by_sbj = M_35x100 %#ok<NOPTS>
search_params =
N_AOIs: 10
N_comp: 3
max_N_comp: 12
sbj_idx: [1x35 double]
trial_idx: [1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28]
N_left_out: 2
Borda_diagnosep: 1
D =
sequences: {35x28 cell}
target: [35x1 double]
SR_params: [1x1 struct]
trial_idx: [1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28]
SR_by_sbj: [35x100 double]
350: Verify that LRaven1_R2_goalfun reproduces the components
%- Call LRaven1_R2_goalfun SR_params = [params.gamma params.lambda_gamma params.lrate] ; %[cvR2,cvR2_train,export] = LRaven1_R2_goalfun(SR_params,D,search_params) %#ok<NOPTS> [cvRMSE,export] = LRaven1_R2_goalfun(SR_params,D,search_params) %#ok<NOPTS> %- Verify that it has indeed used the cached SRs assert(~isfield(export,'SR_by_sbj_by_trial')) ; assert(~isfield(export,'SR_by_sbj')) ; if (divide_std_dev_p) %- Verify that it called SVD on the same DATA matrix assert(max(abs(export.data(:)-data(:)))<TOL) ; %- Verify that it got the same U, Sigma, and PC assert(max(abs(export.U(:)-U(:)))<TOL) ; assert(max(abs(export.PC(:)-PC(:)))<TOL) ; sigma = diag(Sigma) ; assert(max(abs(export.Sigma(:)-sigma(:)))<TOL) ; clearvars sigma %- Verify that it thereby arrived at the same projections assert(max(abs(export.projections(:)-projections(:)))<TOL) ; end % if (~divide_std_dev_p)
cvRMSE =
3.2769
export =
search_params: [1x1 struct]
SR_params: [1x1 struct]
mean_SR_across_sbj: [1x100 double]
std_SR_across_sbj: [1x100 double]
data: [35x100 double]
U: [35x35 double]
Sigma: [35x1 double]
PC: [100x35 double]
projections: [35x35 double]
mean_R2_gain: [1x35 double]
unanim_scores: [1.0417 0.9333 0.8417 0.7500 0.6667 0.5833 0.5000 0.4167 0.3333 0.2500 0.1667 0.0833]
ordered_scores: [0.9483 0.9087 0.8686 0.7537 0.5825 0.5556 0.5237 0.4091 0.3864 0.2602 0.1584 0.1448]
best_idx: [9 1 2 7 6 5 11 4 10 8 12 3]
max_offdiag_corr: [595x1 double]
Borda_winners: [9 1 2]
R2_set: [595x1 double]
R2_train: 0.4230
R2_test: 0.2427
RMSE_train: 2.8067
RMSE_test: 3.2769
360: Are the Borda components the same as the globally selected ones?
LRaven1_R2_goalfun.m calls utils/regression/select_components_Borda.m which institutes an "election" of components across several hundred cross-validation sets (or "voters"). If all goes well, the election winners should match the best_comp above, although this is not a mathematical necessity. See http://en.wikipedia.org/wiki/Borda_count
Borda_winners = export.Borda_winners %#ok<NOPTS> describe(export.max_offdiag_corr) ; % For this data set, the assumption of (approximate) orthogonality holds up % reasonably well -- the average off-diagonal correlations (~0.14) are % unlikely to change the ranks of the R2_gain of the components. % For smaller data sets (fewer subjects), however, the off-diagonal % correlations have been observed to get as high as 0.7, which is a problem. %- If Borda_winners==best_comp, the cross-validation results should match if (all(Borda_winners==best_comp)) if (~divide_std_dev_p) assert(max(abs(cvR.R2_set(:)-export.R2_set(:)))<TOL) ; assert(max(abs(cvR.R2_train-export.R2_train))<TOL) ; assert(max(abs(cvR.R2_test-export.R2_test))<TOL) ; end else fprintf('Borda_winners %s different from global winners %s\n',... mat2str(Borda_winners), mat2str(best_comp)) ; end
Borda_winners =
9 1 2
Mean Std.dev Min Q25 Median Q75 Max
------------------------------------------------------------
0.138 0.047 0.04 0.11 0.13 0.16 0.32
999: Finish
close all %%%%% End of file LR1_SVD_study.m