- Introduction
- Brief Description of DUAL and AMBR
- Simulation Experiment Method
- Results and Discussion
- Conclusion
We performed a simulation experiment to contrast the two ways of
combining access and mapping--parallel vs. serial.
The experiment also tested whether the AMBR model was capable
to access a source analog out of a pool of episodes, and to map
it onto a target situation.
The experiment consisted of two conditions. Both conditions
involved running the model on a target problem.
In the 'parallel condition', AMBR operated in its normal manner
with the mechanisms for access and mapping working in parallel.
In the 'serial condition', the program was artificially forced
to work serially--first to access and only then to map.
The target problem and the content of the long-term memory were
identical in all runs. The topics of interest fell into two
categories--the final mapping constructed by the program and the
dynamics of the underlying computation. The latter was monitored
by recording a set of variables describing the internal state of
the system at regular time intervals throughout each run.
The domain used in the experiment deals with simple tasks in
a kitchen. The long-term memory of the model contains semantic
and episodic knowledge about this domain. It has been coded by
hand according to the representation scheme used in DUAL and AMBR
(Kokinov, 1994c; Petrov, 1997). The total size of the knowledge
base is about 500 agents (300 'semantic' + 200 'episodic').
It states, for example, that water, milk, and tea are all
liquids, that bottles are made of glass, and the relation 'on'
is a special case of 'in-touch-with'. The LTM also stores the
representations of eight situations related to heating and
cooling liquids. Two of these eight situations are most
important for the experiment and are described below together
with the target problem.
- Situation A:
-
There is a cup and some water in it. The cup is on a saucer and
is made of china. There is an immersion heater in the water.
The immersion heater is hot. The goal is that the water is hot.
The outcome is that the water is hot. This is caused by the
hot immersion heater in it.
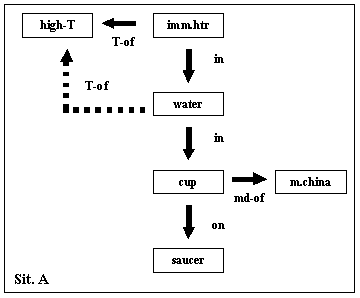
Figure 3.
Schematized representation of situation A.
Objects are shown as boxes and relations with arrows.
Dashed arrows stand for relations in the 'outcome'.
The actual AMBR representation is more complex--it consists of
19 agents and explicates the causal structure (not shown in the
figure). See text for details.
- Situation B:
-
There is a glass and an ice cube on it. The glass is made of
[material] glass. The glass is in a fridge. The fridge is cold.
The goal is that the ice cube is cold.
The outcome is that the ice cube is cold. The fact that it is
on the glass and the glass is in the fridge entails that the
ice cube itself is in the fridge. In turn, this causes the ice
cube to be cold, as the fridge is cold.
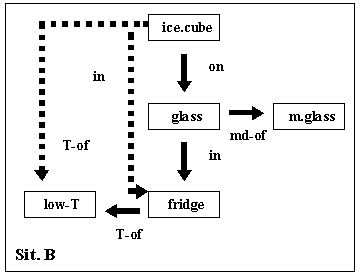
Figure 4.
Schematized representation of situation B.
Dashed arrows stand for relations in the 'outcome'.
The actual AMBR representation is more complex--it consists of
21 agents and explicates the causal structure (not shown in the
figure). See text for details.
- Target Problem (situation T):
-
There is a glass and some coke in it. The glass is on a table
and is made of [material] glass. There is an ice cube in the
coke. The ice cube is cold. The goal, if any, is not represented
explicitly.
What is the outcome of this state of affairs?
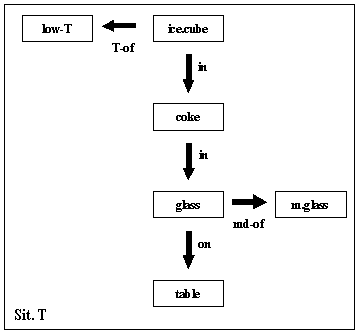
Figure 5.
Schematized representation of the target situation.
The actual AMBR representation is more complex and consists
of 15 agents. See text for details.
As evident from Figures 3,
4, and 5,
both situations A and B may be considered similar
to the target problem. There are some differences, however.
Situation B involves the same objects and relations as
the target but the structure of the two are different.
In contrast, situation A involves different objects but
its system of relations is completely isomorphic to that of the
target. According to Gentner (1989), the pair A-T may
be classified as analogy while B-T as mere appearance.
Thus it was expected that situation B would be easier
to retrieve from the total pool of episodes stored in LTM. On
the other hand, A would be more problematic to retrieve
but once accessed it would support better mapping.
The Common Lisp implementation
of the AMBR model was run two times on the target problem.
The two runs carried out the 'parallel' and the 'serial'
conditions of the experiment, respectively. The contents of
the long-term memory and the parameters of the model were
identical in the two conditions.
Recall that situations have decentralized representations in
AMBR. The target problem was represented by a coalition of 15
agents standing for the ice-cube, the glass, two instances of
the relation 'in' and so on. 12 of these agents were attached
to the special nodes that serve as activation sources in the
model. The attachment was the same in the two experimental
conditions.
In the parallel condition,
the model was allowed to run according to its specification.
That is, all AMBR mechanisms ran in parallel, interacting with
one another. The program iterated until the system reached a
resting state. A number of variables were recorded at regular
intervals throughout the run. Out of these many variables, the
so-called retrieval index is of special interest.
It is computed as the average activation level of the agents
involved in each situation.
In short, at the end of the run we had the final mapping
constructed by the program as well as a log file of the retrieval
indices of all eight situations from the LTM.
In the serial condition,
the target problem was attached to the activation source in
the same way and the same data were collected. However, the
operation of the program was forcefully modified to separate
the processes of access and mapping. To that end, the run was
divided in two steps.
During step one, all mapping mechanisms in AMBR were manually
switched off. Thus, spreading activation was the only mechanism
that remained operational. It was allowed to work until the
pattern of activation reached asymptote. The situation with the
highest retrieval index was then identified. If we hypothesize
a 'retrieval module', this is the situation that it would access
from LTM.
After the source analog was picked up in this way, the experiment
proceeded with step two. The mapping mechanism was switched back
on again but it was allowed to work only on the source situation
retrieved at step one. This situation was mapped to the target.
Thus, at the end of the second run we had the final mapping
constructed at step two, as well as two logs of the retrieval
indices.
In both experimental conditions the model settled in less
than 150 time units and produced consistent mappings.
By 'consistent' we mean that each element of the target problem
was unambiguously mapped to an element from LTM and that all
these corresponding elements belonged to one and the same base
situation. Stated differently, the mappings were one-to-one
and there were no blends between situations.
In the parallel condition,
the target problem was mapped to situation A,
yielding the correspondences in--in, water--coke,
imm.heater--ice.cube, T.of--T.of, high.T--low.T,
made.of--made.of, etc.
Four elements from the source situation remained unmapped and
in particular the agent representing that the water is hot.
This proposition is a good candidate for inference by analogy.
Mutatis mutandis, it could bring the conclusion that the
coke is cold. (In the current version of AMBR the mechanisms
for analogical transfer are not implemented yet.)
In the serial condition,
situation B won the retrieval stage.
This is explained by the high semantic similarity between its
elements and those of the target--both
deal with ice cubes in glasses, cold temperatures, etc.
The asymptotic level of the retrieval index for B was
about four times greater than that of any other situation.
In particular, situation A ended up
with only 5 out of 19 agents passing the working memory
threshold.
According to the experimental procedure,
situation B was then mapped to the target during the
second stage of the run. The correspondences that emerged
during the latter stage are shown in
Table 1.
The semantic similarity constraint has dominated this run.
This is not surprising given the high degree of superficial
similarity between the two situations. There is, however, a
serious flaw in the set of correspondences. The proposition
'T.of (ice.cube, low-T)', which belongs to the
initial state of the target, is mapped to the
proposition 'T.of (ice.cube, low-T)', which is a
consequence in the source. Therefore, the whole
analogy between the target problem and the situation B
could hardly generate any useful inference.
=========================================================
Situation B Target situation
---------------------------------------------------------
ice.cube ice.cube
fridge coke
glass glass
in (ice.cube, fridge) in (ice.cube, coke)
in (glass, fridge) in (coke, glass)
on (ice.cube, glass) on (glass, saucer)
T.of (fridge, low-T) <unmapped>
T.of (ice.cube, low-T) T.of (ice.cube, low-T)
low-T low-T
made.of (glass, m.glass) made.of (glass, m.glass)
m.glass m.glass
initstate1 initstate
initstate2 <unmapped>
interstate table
endstate endstate
goalstate <unmapped>
follows (initst1, endst) follows (initst, endst)
to.reach (initst1, goalst) <unmapped>
cause (initst2, in(i.c, fr)) <unmapped>
cause (interst, T.of(i.c)) <unmapped>
=========================================================
Table 1.
Correspondences constructed by the model in the
serial condition.
To summarize, when the mechanisms for access and mapping worked
together, the model constructed an analogy that can potentially
solve the problem. On the other hand, when the two mechanisms
were separated, the retrieval stage favored a superficially
similar but inappropriate base.
The presentation so far concentrated on the final set of
correspondences produced by the model. We now turn to the
dynamics of the computation as revealed by the time course of
the retrieval indices.
Figure 6 plots the retrieval indices
for several LTM episodes during the first run of the program
(i.e. when access and mapping worked in parallel).
Figure 7 concentrates on the early stage
of the first run and compares it with the second run (i.e. when
only the access mechanism was allowed to work). Note that the
two plots are in different scales.
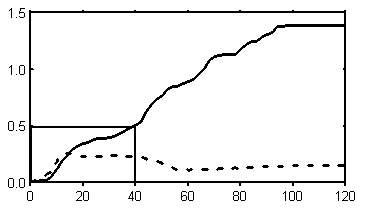
Figure 6.
Plot of retrieval indices versus time for
the parallel condition.
Situation A is in solid line,
B in dashed.
The 'south-west' corner of the plot is reproduced in
Figure 7
with threefold magnification.
These plots tell the following story: At the beginning of the
parallel run, several situations were probed tentatively by
bringing a few elements from each into the working memory.
Of this lot, B looked more promising than any of its
rivals as it had so many objects and relations in common with
the target. Therefore, about half of the agents belonging to
situation B entered the working memory and began trying
to establish correspondences between themselves and the target
agents. The active members of the rival situations were doing
the same thing, although with lower intensity. At about 15 time
units since the beginning of the simulation, however, situation
A (with the immersion heater) rapidly gained strength and
eventually overtook the original leader. At time 40, it had
already emerged as winner and gradually strengthened its
dominance.
The final victory of situation A,
despite its lower semantic similarity compared to
situation B, is due to the interaction
between the mechanisms of access and mapping in AMBR.
More precisely, in this particular case it is the mapping that
radically changes the course of access. To illustrate the
importance of this influence, Figure 7 contrasts the retrieval
indices with and without mapping.
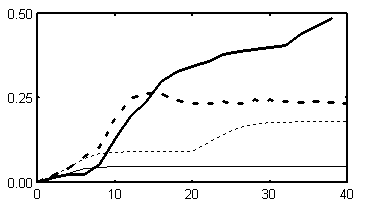
Figure 7.
Retrieval indices for situations A and
B with and without mapping influence
on access.
The thick lines correspond to the parallel condition and
replicate (with threefold magnification) the lines from the
'south-west' corner of Figure 6.
The thin lines show 'pure' retrieval indices.
See text for details.
The thin lines in Figure 7 show the retrieval indices for the
two situations when mapping mechanisms are suppressed. Thus,
they indicate the 'pure' retrieval index of each situation--the
value that is due to the access mechanism alone. The index for
situation B is much higher than that of A and,
therefore, B was used as source when the mapping was
allowed to run only after the access had finished.
The step-like increases of the plots indicate moments in which
an agent (or usually a tight sub-coalition of two or three agents)
passes the working memory threshold. This happens, for example,
with situation B between time 20 and 30 of the serial
condition (the thin dashed line in Figure 7).
Thus, accessing a source episode in AMBR is not an all-or-nothing
affair. Instead, situations enter the working memory agent by
agent and this process extends far after the beginning of the
mapping. In this way, not only can the access influence the
mapping but also the other way around.
In the interactive condition the mapping mechanism boosted the
retrieval index via what we call a
'bootstrap cascade'.
This cascade operates in AMBR in the following way. First, the
access mechanism brings two or three agents of a given situation
into the working memory. If the mapping mechanism then detects
that these few agents can be plausibly mapped to some target
elements, it constructs new correspondence nodes and links in
the AMBR network. This creates new paths for the highly active
target elements to activate their mates. The latter in turn can
then activate their 'coalition partners', thus bringing a few
more agents into the working memory and so on.
The bootstrap cascade is possible in AMBR due to two important
characteristics of this model. First, situations have
decentralized representations which may be accessed piece by
piece. Second, AMBR is based on a parallel cognitive architecture
which provides for concurrent operation of numerous interacting
processes. Taken together, these two factors enable seamless
integration of the subprocesses of access and mapping in
analogy-making.
The simulation experiment reported in this paper provides a
clear example of mapping influence on analog access and of the
advantages of the parallel interactionist view on analogy-making.
Furthermore, the computational model AMBR provides a theoretical
framework for explaining the controversies in the psychological
data on access and reminding. It is possible to explore in which
cases the interaction between access and mapping produces results
different from a sequential and independent processing. It provides
also a framework for generating more precise hypotheses and new
experimental designs for their testing. Thus, for example, the
detailed logs of the running model might be used for comparison
with protocols of think-aloud experiments.
Analogy-making has certainly no clear cut boundaries. Most
literature has concentrated on explicit analogies, i.e.
consciously retrieving an analog and noticing the analogy.
However, there are other cases which might be called implicit
or partial analogies, e.g. subconsciously accessing part of a
previously solved problem and mapping it to part of the target
description without consciously noticing the analogy. However,
there are other cases which might be called implicit or partial
analogies, e.g. subconsciously accessing part of a previously
solved problem and mapping it to part of the target description
without consciously noticing the analogy.
The decentralized representations of situations in AMBR make
it possible to model the process of partial access, access with
distortions, blending (Turner & Fauconnier, 1995), and
interference. A previously solved problem can influence the
course of problem solving in an even more subtle way by priming
some concepts or situations which then trigger a particular
solution (Kokinov, 1990; Schunn & Dunbar, 1996).
The AMBR model can be used to analyze such cases. It has already
been successfully applied for predicting priming and context
effects (Kokinov, 1994c).
Priming effects are an example of the influence of access on
mapping which is the opposite direction of the one discussed in
the current paper. Order effects are another kind of effect that
goes in 'forward' direction. Such effects may be due to
non-simultaneous perception of the elements of the target
problem (Keane, Ledgeway, & Duff, 1994) and/or non-simultaneous
retrieval of relevant pieces of information from LTM.
Thus the mutual influence between analog access and mapping
offers many opportunities for investigation.
Falkenhainer, B., Forbus, K., & Gentner, D. (1986).
The structure-mapping engine.
Proceedings of the Fifth Annual Conference on
Artificial Intelligence.
Los Altos, CA: Morgan Kaufman.
Forbus K., Gentner D., & Law, K (1995).
MAC/FAC: A model of similarity-based retrieval.
Cognitive Science, 19, 141-205.
French, R. (1995).
The Subtlety of Sameness:
A Theory and Computer Model of Analogy-Making.
Cambridge, MA: MIT Press.
Gentner, D. (1983).
Structure-mapping: A theoretical framework for analogy.
Cognitive Science, 7, 155-170.
Gentner, D. (1989).
The mechanisms of analogical learning.
In S. Vosniadou and A. Ortony (Eds.),
Similarity and analogical reasoning.
New York, NY: Cambridge University Press.
Gick, M.L. & Holyoak, K.J. (1980).
Analogical problem solving.
Cognitive Psychology 12 (80), 306-356.
Hofstadter, D. & the Fluid Analogies Research Group (1995).
Fluid Concepts and Creative Analogies: Computer models
of the fundamental mechanisms of thought.
New York: Basic Books.
Holyoak K. & Koh K. (1987).
Surface and structural similarity in analogical transfer.
Memory and Cognition, 15 (4), 332-340.
Holyoak K. & Thagard P. (1989).
Analogical mapping by constraint satisfaction.
Cognitive Science, 13, 295-355.
Holyoak, K. & Thagard, P. (1995).
Mental leaps: Analogy in creative thought.
Cambridge, MA: MIT Press.
Hummel, J. & Holyoak, K. (1997).
Distributed representation of structure:
A theory of analogical access and mapping.
Psychological Review, 104, 427-466.
Keane, M., Ledgeway, K., & Duff, S. (1994).
Constraints on analogical mapping:
A comparison of three models.
Cognitive Science, 18, 387-438.
Kokinov, B. (1988).
Associative memory-based reasoning:
How to represent and retrieve cases.
In T. O'Shea and V. Sgurev (Eds.),
Artificial intelligence III:
Methodology, systems, applications.
Amsterdam: Elsevier.
Kokinov, B. (1990).
Associative memory-based reasoning: Some experimental results.
Proceedings of the Twelfth Annual Conference of the
Cognitive Science Society.
Hillsdale, NJ: Lawrence Erlbaum Associates.
Kokinov, B. (1994a).
The context-sensitive cognitive architecture DUAL.
Proceedings of the Sixteenth Annual Conference of the
Cognitive Science Society.
Hillsdale, NJ: Lawrence Erlbaum Associates.
Kokinov, B. (1994b).
The DUAL cognitive architecture: A hybrid multi-agent approach.
Proceedings of the Eleventh European Conference of
Artificial Intelligence.
London: John Wiley & Sons, Ltd.
Kokinov, B. (1994c).
A hybrid model of reasoning by analogy.
In K. Holyoak & J. Barnden (Eds.),
Advances in connectionist and neural computation theory.
Vol. 2: Analogical connections (Chapter 5, pp. 247- 318).
Norwood, New Jersey: Ablex.
Kokinov, B., Nikolov, V., & Petrov, A. (1996).
Dynamics of emergent computation in DUAL.
In A. Ramsay (Ed.),
Artificial intelligence: Methodology, systems,
applications (pp. 303-311).
Amsterdam: IOS Press.
Kuhn, T. S. (1970).
The Structure of Scientific Revolutions
(second ed., enlarged).
Chicago: The University of Chicago Press.
(First edition published 1962.)
Minsky, M. (1986).
The society of mind.
New York: Simon and Schuster.
Mitchell, M. (1993).
Analogy-making as perception: A computer model.
Cambridge, MA: MIT Press.
Petrov, A. (1997).
Extensions of Dual and Ambr.
Unpublished M.Sc. Thesis.
New Bulgarian University, Cognitive Science Department.
Ross, B. (1989).
Distinguishing types of superficial similarities:
Different effects on the access and use of earlier problems.
Journal of Experimental Psychology:
Learning, Memory, and Cognition, 15, 456-468.
Ross, B. & Kilbane, M. (1997).
Effects of principle explanation and superficial similarity
on analogical mapping in problem solving.
Journal of Experimental Psychology:
Learning, Memory, and Cognition, 23 (2), 427-440.
Ross, B. & Sofka, M. (1986).
[Remindings: Noticing, remembering, and using specific
knowledge of earlier problems].
Unpublished manuscript.
Schunn, C. & Dunbar, K. (1996).
Priming, analogy, and awareness in complex reasoning.
Memory and Cognition, 24, 271-284.
Thagard, P., Holyoak, K., Nelson, G., & Gochfeld, D. (1990).
Analog retrieval by constraint satisfaction.
Artificial Intelligence, 46, 259-310.
Turner, M. & Fauconnier, G. (1995).
Conceptual integration and formal expression.
Metaphor and Symbolic Activity, 10 (3), 183-204.
Wharton, C., Holyoak, K., & Lange, T. (1996).
Remote analogical reminding.
Memory and Cognition, 24 (5), 629-643.
 Page maintained by
Alex Petrov
Page maintained by
Alex Petrov
Created 1999-06-26, last updated 2005-11-30.




