| Alexander A. Petrov | Boicho N. Kokinov |
|---|---|
| Department of Psychology Carnegie Mellon University |
CEE Center for
Cognitive Science New Bulgarian University |
| A camera-ready version of this document is available in pdf format (102K). |
|
Copyright note: This paper has been published in the proceedings of the Sixteenth International Joint Conference on Artificial Intelligence (IJCAI-99). The entire copyright in the paper belongs to the International Joint Conference on Artificial Intelligence, Inc. In return for this right, IJCAI has granted to the authors royalty-free permission to reproduce the above paper for the authors' personal use and to post the paper in electronic format on the authors' own World-Wide Web pages. Reproduction of this paper on other servers constitutes violation of applicable laws.
This article explores the advantages and one potential implementation of a new style of computation in which multiple lines of symbolic processing are pursued at different speeds within a hybrid multi-agent system. The cognitive architecture DUAL consists of small hybrid computational entities called DUAL agents. Each agent has a symbolic processor capable of simple symbol manipulations. There is also an activation level associated with each agent. Activation spreads according to connectionist rules. The speed of each symbolic processor is proportional to the activation level of the corresponding DUAL agent and varies dynamically. Thus multiple candidate-solutions to a given problem can be explored in parallel. More computational resources are dedicated to the more promising candidates and the degree of 'promise' is re-evaluated dynamically. This allows for flexible and efficient behavior of the system as a whole. The exact relationship between symbolic speed and connectionist activation is based on an energetic analogy. The symbolic processor is conceptualized as a machine converting connectionist activation into symbolic work. A language for implementing variable-speed symbol manipulations using delayed evaluation is introduced: S-Lisp. A small example from a DUAL-based cognitive model, illustrates variable-speed marker passing in a semantic network.
There are two challenges that any computational system operating in a complex environment must face--flexibility and efficiency. Stated in general terms, the environment presents some problems (or tasks) to the system, which in turn has to generate solutions (or behaviors). Under this formulation, flexibility implies that the set of potential solutions to any given problem should be as large and open-ended as possible. No options should be ruled out a priori. At the same time, the pressure for efficiency restricts the number of candidate-solutions that can actually be considered in any particular case.
Each of these requirements is hard enough in itself but the conjunction of the two is even more demanding because they push in opposite directions. This dual challenge has been addressed in various ways ranging from the exhaustive backtracking of the early AI programs, to heuristic search (Newell and Simon, 1976) and hill climbing, to the elaborate control strategies of modern cognitive architectures such as ACT-R (Anderson and Lebiere, 1998) and SOAR (Newell, 1990).
One approach (Hofstadter, 1983; Hofstadter, 1995; Kokinov, 1994a) to the flexibility/efficiency challenge rests on the following four ideas: (i) Multiple candidate-solutions are considered in parallel. (ii) There is a very cheap mechanism that calculates rough on-line estimates of the 'promise' of each candidate. (iii) The computational resources of the system are allocated unevenly among the candidates, favoring the more promising ones. (iv) Promise estimates are updated constantly, taking into account whatever new information becomes available and re-allocating the computational resources accordingly.
Spreading activation is one mechanism that seems ideally suited for points (ii) and (iv) above. It is cheap, runs continuously, and can poll information from various sources dynamically. On the other hand, many tasks require complex, structured, and hierarchically organized representations. Taken together, this suggests a hybrid symbolic/connectionist system. Such hybrid systems have a number of desirable properties (Dinsmore, 1992; Sun and Alexandre, 1997).
This article builds on the hybridization idea ( Kokinov, 1997) and concentrates on the interface between the symbolic and the subsymbolic. The main idea is to have multiple symbolic processors running at variable speed. The speed is proportional to the activation level attached to each processor and estimating the 'promise' of the candidate-solution that the processor is working upon. This concretizes the general point (iii) above. The speed varies dynamically, as the activation level varies.
The next section begins with a brief overview of some alternative proposals from the literature. The variable-speed idea is then described in detail, followed by an illustrative example from an implemented simulation.
Symbol manipulation is done in discrete steps. The algorithm describing a symbolic process usually involves branching and loops, but during the execution it unfolds into a linear sequence of steps. As a first approximation, it may be assumed that all steps are of equal 'length'. (This approximation will be refined later on.) Thus the speed of a symbolic process can be defined as the number of steps advanced during a given time interval.
Conventional multi-tasking operating systems support multiple processes running in parallel. A single physical processor serves all processes in turn by time-sharing. Different priorities can be assigned to control the number of time slices allotted to a given process. This scheme can easily be adapted to use activation levels as priorities. However, it requires a centralized task manager and hence hinders the self-organizing kind of parallelism that is of interest here.
In production systems (Newell, 1973, 1990; Anderson, 1983), the equivalent of a symbolic step is called a production. There are production systems that use the notion of activation (Anderson, 1983; Just and Carpenter, 1992). The cognitive architecture ACT-R (Anderson and Lebiere, 1998) is a representative example. Productions in ACT-R operate on declarative memory elements called chunks. There is an activation level associated with each chunk and a strength value for each production. These subsymbolic parameters are used by the conflict resolution mechanism to select (stochastically) which production fires on a given cycle. Moreover, the time to execute a production depends on the activation of the chunk(s) that have matched its condition(s). This temporal relationship is used to predict reaction time data from psychological experiments. The timing, however, is not used to control the processing within the architecture itself. The control is based on a goal stack and only the productions that match the chunk at the top of the stack are considered for firing. Thus there is little parallelism at the level of global symbolic processes. Rather, a single process is carried out by manipulating the single goal stack.
In the models of Douglas Hofstadter and his collaborators (Hofstadter, 1983, 1995; Mitchell, 1993; French, 1995) the equivalent of a symbolic step is called a codelet. Many such codelets wait in a repository called the coderack and vie for a chance to run. Codelets tend to form chains--when a codelet is executed, it posts one or more successors to the coderack. Each such chain corresponds to a symbolic process. The coderack contains codelets belonging to different chains, thus emulating parallelism. An urgency value is assigned to each codelet. These urgencies depend on various things, including activation levels. On each cycle, a codelet is chosen from the coderack and run. The choice is probabilistic but not uniformly random--it is biased in favor of codelets with higher urgencies. When this sampling is repeated many times, the overall effect is that all symbolic processes (i.e. chains) advance in parallel at speeds proportional to the average urgency of the respective codelets.
A very interesting feature of this scheme is the so-called computational temperature. It is a global parameter controlling the degree of randomness in the system. The temperature modulates the strength of the bias that the urgencies introduce into the coderack. At intermediate temperatures the probability of selecting a given codelet is roughly linearly related to its urgency. At high temperatures, however, all codelets have approximately equal chances to run regardless of their urgencies. By contrast, at low (freezing) temperatures the bias becomes overwhelming and the most urgent codelet is chosen almost deterministically. There are specialized codelets that measure the temperature and change it dynamically.
Restated in terms of speed, the Hofstadter's proposal allows for parallel symbolic processes running at different speeds. The speed can be controlled both by local factors (urgencies) and a global one (temperature). Both kinds of factors vary dynamically.
Sometimes, however, a phenomenon called urgency explosion occurs in the coderack (French, 1995). It is analogous to inflation in economics and occurs when many new codelets of high urgency are posted to the coderack, thus inflating the urgencies of the old codelets waiting therein. The urgency explosion has undesirable consequences and special measures must be taken to prevent it (French, 1995).
Finally, the task of designing a system in which parallel symbolic processes run at variable speed may be addressed in a straightforward manner. The cognitive architecture DUAL (Kokinov, 1994a, 1994b) represents such an attempt. It consists of a population of small computational entities called DUAL agents. Each agent is hybrid and has a symbolic and a connectionist aspect. The symbolic aspect consists of a micro-frame and a symbolic processor. The connectionist aspect is analogous to a unit in a neural network. The micro-frame is a bundle of labeled slots filled with references to other agents. The agent interacts with the agents referenced in its micro-frame by sending them messages and activation. An activation level is associated with each DUAL agent and the interactions between the agents can be regarded as links. The activation level of a given agent represents the system's internal estimate of its relevance to the problem being solved, the surrounding context, etc. It changes dynamically as these factors change. A threshold is imposed on the activation so that the agents that fail to reach some minimal degree of relevance are kept dormant.
The symbolic processor of each agent runs at a speed proportional to its activation level. Thus very active agents run rapidly and determine the overall flow of computation, moderately active agents run slowly, and inactive agents do not run at all. All agents above the threshold run in parallel and there is no central executive in the system to coordinate their work. Rather, coordination and global consistency are achieved by massive local interactions: both symbolic (exchange of messages) and connectionist (exchange of activation). The behavior of the system as a whole emerges out of these local activities. This style of dynamic emergent computation allows for great flexibility, efficiency, and context sensitivity (Kokinov et al., 1996).
The presentation so far simply postulated that the symbolic processors in DUAL run at a speed proportional to the activation level of the corresponding agent. The next two sections concretize this abstract specification.
The exact relationship between symbolic speed and connectionist activation in the architecture DUAL rests on the following energetic analogy: the manipulation of symbols can be conceptualized as work and the connectionist activation as power. Doing work requires energy, which is supplied to the symbolic processor by the connectionist aspect of the agent. The energy is calculated by integrating the power over time. The speed of the symbolic computation depends on the power (i.e. the activation level). The same amount of work is completed rapidly when there is plenty of power, slowly when power is scarce, and not at all if it is lacking completely.
The symbolic processing in the architecture can be categorized into segments of increasing complexity (Petrov, 1998). (i) A symbolic operation is the smallest unit of symbol manipulation. The operations are simple, atomic, and deterministic. They are the elementary instructions of the symbolic processor. (ii) A symbolic step is a sequence of operations performed by a single agent without intervening symbolic interactions with other agents. (iii) A rigid symbolic process is a fixed and a priory specified sequence of steps performed by a single agent. There may be intervening interactions. (iv) An emergent symbolic process is distributed over a coalition of interacting agents. It does not have any complete a priory specification. Rather, the course of computation is determined dynamically by the interplay of various pressures (Kokinov et al., 1996).
Each symbolic operation is characterized by some consumption C. This is a real number specifying the amount of symbolic work embedded in the operation. Different operations may have different consumptions. They are free parameters of the particular model and may be fixed on theoretical grounds and/or estimated from empirical data. This scheme offers considerably more freedom than the alternative proposals that typically assume equal consumption for all operations.
If a fine-grained analysis at the level of individual operations is not warranted, consumptions may be specified at the level of symbolic steps. The latter are often more convenient due to their larger grain size. A symbolic step is performed by a single agent and by definition there is no symbolic exchange with other agents during the step. Thus as far as the inter-agent communication is concerned, steps can be treated as units, disregarding the constituent operations. What matters is the final outcome (in the form of a message send to another agent) and the timing of its appearance.
Each symbolic processor acts as a machine that transforms connectionist energy into symbolic work. Not all energy, however, is converted into useful work. There is some overhead for covering the internal needs of the processor itself. The efficiency coefficient eta is defined as the ratio of the useful work A to the total energy input E: eta=A/E. This coefficient characterizes the symbolic processor. Different processors can have different efficiencies. In a cognitive model, for instance, processors performing highly automated tasks have eta close to 1 while processors performing novel tasks have low efficiency. The efficiency can even be adjusted dynamically by some kind of learning--the basic rule is that it increases with practice.
Suppose a symbolic processor starts working on some operation (or step) at time t0. The amount of energy needed for the operation can be calculated in advance--it is E=C/eta, where C is the consumption of the operation. This energy must be provided by the connectionist aspect of the agent. This takes time, as the rate of supply is limited. The energy function that describes the accumulation of energy in time is defined by the integral:
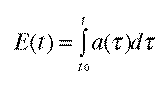
where a(tau) is the activation level. Activation levels in DUAL must be above some positive threshold in order for the symbolic processor to work. (If a(tau) drops below the threshold even for a moment, the symbolic processing is aborted and all intermediate results are lost.) Because a(tau) is always positive, E(t) is an increasing function and thus has an inverse E-1. The inverse function expresses the time needed to produce a given amount of energy.
Putting all pieces together, the exact moment in which the symbolic operation is completed is t = t0 + E-1(C/eta). The outcome of the operation becomes available at that moment. It may be a message sent to another agent or a modification of the internal micro-frame. Then the processor moves to the next operation as prescribed by the algorithm and the whole cycle repeats.
When the symbolic processor is idle, all energy produced by the connectionist aspect of the agent goes unused. It cannot be accumulated. In other words, it is not allowed to amass energy 'on store' and then expend it all at once, thus attaining very high peak power.
The energetic analogy offers the following advantages: (i) It provides for variable-speed symbolic computation and hence for all associated benefits. Indeed, it is clear that the specification described in this section implies that the more active agents run more rapidly. (ii) The activation levels can change dynamically and all changes have instant effect. (iii) The architecture DUAL has a well-defined notion of time. It is measured on a continuous scale and frames the occurrence of all symbolic events. (iv) The speed of each DUAL agent is defined independently of that of the other agents. Thus the architecture can be run without any modification on parallel hardware. (v) The relationship between symbolic speed and connectionist activation is specified without recourse to any particular implementation. (vi) Symbolic processes can be finely parameterized and the parameters have straightforward interpretation--consumptions and efficiency coefficients.
The DUAL architecture has been fully implemented. All programs are written in Common Lisp using CLOS. An extension of Lisp called S-Lisp ('suspendable' Lisp) has been developed (Petrov, 1998) for the purposes of the variable-speed symbolic computations. A rudimentary compiler translates S-Lisp programs into 'plain' Lisp. This section outlines the main features of the language and the principles of its implementation.
S-Lisp is an extension of Common Lisp. Its main difference from plain Lisp is that it supports four additional special operators: s-progn, s-eval, s-values, and suspended-value-bind. They are 'suspendable' analogs to the respective Lisp operators. S-Lisp also supports most (but not all) 'plain' Lisp primitives such as progn, if, let, and setq. The language also supports function calls and recursion, which in turn allows for loops.
S-progn establishes a sequence of symbolic steps to be executed at variable speed by the processor of some DUAL agent called a host. The complementary suspension primitive, s-eval, signals that a given S-Lisp form is suspendable and announces the amount of energy needed for it. The two suspension primitives go together. s-eval may appear only within the lexical scope of an s-progn; it is an error elsewhere. Conversely, s-progn is like an ordinary progn in all respects except the treatment of s-eval and the other suspension primitives. A very simple S-Lisp program is illustrated below:
(s-progn host
(s-eval 0.5 (prepare x))
(when (s-eval 0.2 (check x))
(s-eval 2.5 (work-on x)))
(s-eval 0.1 (cleanup)) )
The remaining two suspension primitives, s-values and suspended-value-bind, are used to export and import values from functions defined via s-progn.
The implementation of s-progn and s-eval is based on delayed evaluation. While the theoretical specification of DUAL postulates that symbolic processes run smoothly and at variable speed, the implementation carries them out in instantaneous jumps. Pauses are imposed between the jumps to produce the timing postulated by the theory.
When a processor begins working on some symbolic operation, it does not actually execute it. Instead, it wraps it in a closure and stores it on a stack. One such stack is maintained for each processor (i.e. DUAL agent). There is an energy balance associated with each stack. The energy balance is equal to the difference between supplied and consumed energy. When the balance is negative, the processor waits until it becomes positive. On each connectionist cycle, the connectionist machinery increases the balance with some small amount depending on the activation level and the efficiency coefficient of the host. After some time, the balance becomes positive and the top closure on the stack is popped and executed.
The S-Lisp compiler analyzes the source code, traps all occurrences of s-eval and replaces them with 'plain' Lisp forms that generate closures and arrange them on the stack. The stack is established by the enclosing s-sprogn form. The top-level loop of the implementation checks the stacks of all active DUAL agents and pops the ones with positive energetic balance. This scheme also supports the parallel work of multiple agents.
S-Lisp programs should be written with care because many intuitions from 'plain' Lisp are violated. In particular, s-progn does not return any useful value. This is because a call to s-progn does not execute the forms in its body; it delays them. Thus the value that the programmer expects will be computed later, long after the original call to s-progn is over. s-values must be used to export a value out of a suspendable function and this value must be bound via suspended-value-bind.
A mailbox technique is used to transfer suspended values through destructive operations executed as side effects. A mailbox is a data structure containing a field that can be modified destructively. The job of s-values is to make a new empty mailbox and to arrange that the suspended value (or multiple values) will be stored in it when the suspended computation is completed. The job of s-progn is to catch the mailbox, open it at the appropriate time, and bind the values to local variables accessible within its lexical scope.
This final section provides an example of variable-speed
symbolic processing in action. It also illustrates the utility of
symbolic/connectionist hybridization. The material for the
example is taken from actual simulation experiments with a
DUAL-based cognitive model called AMBR
(
Kokinov, 1994a; Petrov, 1998). In these simulations AMBR
tries to solve simple everyday problems such as:
"There is some milk in a teapot. There is also a hot plate.
The goal is to heat the milk."
The model solves these problems by analogy to
previous cases. The long-term memory of the system contains a
number of past problems with solutions. It also contains semantic
knowledge about general regularities in the domain. When faced
with a new target problem, AMBR attempts to retrieve an
appropriate source analog, map it to the target, and transfer the
solution. Several such retrievals and mappings are attempted in
parallel and at variable speed.
AMBR, like all DUAL-based models, consists entirely of DUAL agents. They carry out all representational and computational functions in the system. The long-term memory is just a population of interacting agents. Some of them, the so-called concept-agents, represent classes of objects such as milk, water, and liquid. These agents form the backbone of AMBR's semantic memory. There are also instance-agents standing for individual instances such as milk-8. The agents form coalitions to represent propositions (e.g. in-6(milk-8, teapot-3)) and episodes. Finally, hypothesis-agents are created during the problem-solving process to represent tentative correspondences such as milk-8<->water-3.
Note that these are not passive data structures. Rather, each agent is a semi-autonomous entity that heavily interacts with its peers. For instance, the agent milk sends symbolic messages and connectionist activation to the agent liquid. The symbolic processor of liquid then handles and re-sends these messages at variable speed according to the principles discussed above.
For the sake of concreteness, the example here concentrates on
one of the several computational mechanisms used in AMBR. The
marker passing mechanism stems from the semantic network
tradition (see Hendler (1988) for an overview). In its most basic
form it is a tool for answering the question:
"Given two nodes in a semantic network,
is there a path connecting them?"
The underlying idea is simple--the two nodes of origin are
marked. They then mark their neighbors, which in turn mark
further. If the two 'waves' of markers intersect, a path is
found. AMBR uses these intersections to build hypotheses about
similarity-based correspondences between instance agents.
Consider the following coalition:
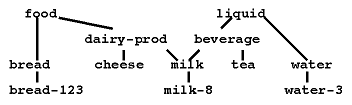
The words in the figure denote agents. The lines denote interactions, usually bi-directional. The agents at the bottom row are instances; all others are concepts. Note that milk treats two different agents as 'parents'.
Marker passing in AMBR goes hand in hand with spreading activation. Suppose milk-8 is a newly created agent participating in the representation of the target problem and that all other agents in the figure are dormant (i.e. with zero activation) in the long-term memory. Milk-8, being related to the goal, is a strong activation source. It spreads this activation to the agents referenced in its micro-frame. One such agent is the parent concept milk. This input from milk-8 brings its activation level above the critical threshold and it enters the working memory (WM) of AMBR. In turn, milk activates other agents. The coalition gradually enters the WM:
T=0.04, MILK enters WM. T=0.20, BEVERAGE enters WM. T=0.24, DAIRY-PROD enters WM. T=0.42, LIQUID enters WM. T=0.54, CHEESE enters WM. T=0.56, TEA enters WM. T=0.56, FOOD enters WM. T=0.70, WATER enters WM. T=0.92, WATER-3 enters WM. T=0.92, BREAD enters WM. T=1.24, BREAD-123 enters WM. ...
Note that the two branches of the hierarchy receive unequal amounts of activation. This is due to both permanent and transient factors. The permanent factors reflect domain knowledge and are embodied in the 'weights' of the interactions. For example, milk may send more activation to beverage than to dairy-prod. The transient factors are due to goal-related, context, and priming effects. In the above example, the target problem involves a teapot that indirectly activates liquid via the liquid-holder agent (not shown in the figure). All these factors vary across and within problem-solving episodes. The pattern of activation over the population of agents changes dynamically, as the estimated relevance of each agent varies.
The stage is now ready for the marker-passing mechanism per se. Whenever an instance-agent enters the working memory it sends a marker to its parent concept(s). The concept-agents in turn spread the markers to their superclass(es). Each marker carries a reference to the instance-agent that originated it as well as a color tag indicating whether the origin is a target agent. The following transcript illustrates the marker passing process:
T=0.14, #<M1 milk-8> received in MILK. T=0.30, #<M1 milk-8> received in BEVERAGE. T=0.50, #<M1 milk-8> received in DAIRY-PROD. T=0.60, #<M1 milk-8> received in LIQUID. T=0.88, #<M1 milk-8> received in FOOD. T=1.14, #<M2 water-3> received in WATER. T=1.34, #<M2 water-3> received in LIQUID. T=1.54, #<M2 bread-123> received in BREAD. T=1.58, LIQUID detects marker intersection. ...
When two markers of different colors meet in some concept-agent, the latter detects the intersection and initiates a sequence of interactions with various agents that ultimately results in creating a new hypothesis. In our example this would be milk-8<->water-3. Alternative hypotheses (e.g. milk-8<->bread-123) are being constructed in parallel. The respective agents, however, are less active and hence handle their markers more slowly. The net effect is that the population of agents as a whole explores various paths in parallel at speed proportional to their dynamically estimated 'promise'. In a different context, the same agent milk could be mapped to another instance-agent retrieved from some other past episode. There is a vast number of possibilities but only a few of them are considered in any given case.
One of the biggest issues in marker-passing systems is the attenuation of the marking. Without such attenuation there would be too many intersections, most of which are useless and overwhelm the useful ones. Several attenuation strategies have been explored over the years (reviewed by Hendler (1988)): limitation of the number of links each marker can traverse, checks of the outbranching factor of 'promiscuous nodes', etc. In AMBR there is no need for any ad-hoc attenuation mechanism as it follows naturally from the architectural principles of DUAL. Two such attenuation factors are relevant here: (i) The markers cannot reach the agents that have been left totally inactive by the spreading activation mechanism. (ii) Marker passing, as any other symbolic activity in the architecture, depends on the speed of the symbolic processors handling the markers. As a consequence, the markers move rapidly through the 'promising' portions of the semantic memory and then slow down as they reach the periphery of the area delineated by activation levels. The net effect of these and other similar factors is that marker intersections are reported in a temporal order reflecting their potential usefulness for the particular task and the particular context.
It is worthwhile to stress that the global marker passing is a dynamic emergent process. A whole coalition of DUAL agents is needed to cooperatively produce the final result. Each individual agent does local marker passing only. The overall result is determined by a multitude of factors (or 'pressures') each of which has relatively minor impact on its own. Moreover, the strength of these factors varies dynamically in response to various external and internal events. The variable-speed symbolic processing and the energetic analogy presented in this paper are instrumental for these desirable properties.
Anderson, J.R. (1983). The architecture of cognition. Cambridge, MA: Harvard University Press.
Anderson, J.R. & Lebière, C. (1998). The atomic components of thought. Mahwah, NJ: Lawrence Erlbaum Associates.
Dinsmore (1992). The symbolic and connectionist paradigms: Closing the gap. Hillsdale, New Jersey: Lawrence Erlbaum Associates.
French, R. (1995). The subtlety of sameness: A theory and computer model of analogy-making. Cambridge, MA: MIT Press.
Hendler, J. (1988). Integrating marker-passing and problem-solving: A spreading-activation approach to improved choice in planning. Hillsdale, NJ: Lawrence Erlbaum Associates.
Hofstadter, D. (1983). The architecture of Jumbo. In R. Michalski, J. Carbonell, & T. Mitchell (Eds.), Proceedings of the International Machine Learning Workshop (pp. 161-170). Urbana: IL: University of Illinois.
Hofstadter, D. and the Fluid Analogies Research Group (1995). Fluid concepts and creative analogies: Computer models of the fundamental mechanisms of thought. New York: Basic Books.
Just, M. & Carpenter, P. (1992). A capacity theory of comprehension: Individual differences in working memory. Psychological Review, 99 (1): 122-149.
Kokinov, B. (1994a). A hybrid model of reasoning by analogy. In K. Holyoak & J. Barnden (Eds.), Advances in connectionist and neural computation theory. Vol. 2: Analogical connections (Chapter 5, pp. 247- 318). Norwood, New Jersey: Ablex.
Kokinov, B (1994b). The DUAL cognitive architecture: A hybrid multi-agent approach. Proceedings of the Eleventh European Conference on Artificial Intelligence. John Wiley & Sons, Ltd.
Kokinov, B. (1997). Micro-level hybridization in the cognitive architecture DUAL. In R. Sun and F. Alexandre (Eds.), Connectionist-symbolic integration: From unified to hybrid architectures. Hillsdale, NJ: Lawrence Erlbaum Associates.
Kokinov, B., Nikolov, V., & Petrov, A. (1996). Dynamics of emergent computation in DUAL. In A. Ramsay (Ed.), Artificial intelligence: Methodology, systems, applications (pp. 303-311). Amsterdam: IOS Press.
Mitchell, M. (1993). Analogy-making as perception: A computer model. Cambridge, MA: MIT Press.
Newell, A. (1973). Production systems: Models of control structures. In W. Chase (Ed.), Visual information processing (pp. 463-526). New York: Academic Press.
Newell, A. (1990). Unified theories of cognition. Cambridge, MA: Harvard University Press.
Newell, A. & Simon, H. (1976). Computer science as empirical inquiry: Symbols and search. Communications of the ACM, 19: 113-126.
Petrov, A. (1998). A dynamic emergent computational model of analogy-making based on decentralized representations. Unpublished doctoral dissertation, New Bulgarian University, Sofia.
Sun, R. & Alexandre, F. (Eds.), (1997). Connectionist-symbolic integration: From unified to hybrid architectures. Hillsdale, NJ: Lawrence Erlbaum Associates.
| [ Kokinov's Home Page ][ Kokinov's Publications ] | |
| [ Petrov's Home Page ][ Petrov's Publications ] | |
| [ DUAL Main Page ] | [ Get pdf file ] |
| [ AMBR Main Page ] | [ Back to top ] |