The slides for the conference presentation are also available (pdf 127K).
| Alexander A. Petrov | John R. Anderson |
|---|---|
| Department of Psychology Carnegie Mellon University |
Department of Psychology Carnegie Mellon University |
|
A camera-ready version
of this document is available in pdf format (38K). The slides for the conference presentation are also available (pdf 127K). |
|
This paper attempts to draw a bridge between psychophysics and memory research by proposing a memory-based model of category rating. The model is based on the cognitive architecture ACT-R and uses anchors stored in memory that serve as prototypes for the stimuli classified within a response category. The anchors are retrieved by a partial matching mechanism and updated dynamically by an incremental learning mechanism. Anchors also have base-level activations that reflect the frequency and recency of the responses. These mechanisms give rise to sequential effects and nonuniform response distributions. A psychological experiment involving category rating of physical length is reported and the predictions of the model are compared against the empirical data. The psychophysical implications of the model are discussed.
Category rating is a widely used method of data collection in experimental psychology. A category-rating situation arises whenever the participants are asked to assign each stimulus to one of several ordered categories such as 1, 2, ..., 9 or very dissimilar, ..., very similar. Procedures of this kind are common for many studies ranging from psychophysical scaling to similarity judgment to personality inventories. Therefore a detailed analysis of the cognitive mechanisms underlying this task is potentially relevant to a diverse set of situations.
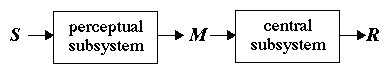
Figure 1. Simplified decomposition of the category-rating process. The external stimulus S maps to an internal magnitude M which in turn gives rise to the overt response M.
A rough decomposition of the process of category rating is presented in Figure 1. (This diagram is by no means complete or accurate; it is provided for expository purposes only.) The perceptual subsystem maps the external stimulus S onto an internal representation M on a psychological continuum. In this paper the internal representation is called magnitude. The magnitude M then serves as a basis for generating an overt response R on the category scale. The latter transformation is the responsibility of the central (or cognitive) subsystem. Both subsystems are characterized with internal states that unfold in time and may differ from trial to trial. Thus each box in Figure 1 has underlying dynamics and the whole system is more complex than the open-loop pipeline suggested by the diagram.
The present paper focuses on the central subsystem and the computational mechanisms converting subjective magnitudes into external reports. While the perceptual aspects of the process are certainly important, they are not central to the research reported here. Therefore the research strategy has been to try to minimize the contribution of the perceptual subsystem so that the properties of the central one can show through. This dictated the choice of a modality for which the perceptual transformation is as simple as possible--physical length.
The empirical relation between stimulus intensities S and averaged category ratings R tends to follow a power function: R = k.Sn (Stevens, 1957). The exponent n is characteristic of the perceptual modality. For physical length, this exponent is very close to 1.0 (Stevens, 1957). In other words, the scale is linear. Thus it seems reasonable to assume that the perceptual subsystem delivers veridical representations of physical length, with little if any systematic distortions (Krantz, 1972). Under this assumption, any patterns in the category-rating data for length are largely due to the central subsystem.
The psychophysical literature reports several phenomena related to category rating. The most basic finding is that the participants are able to perform this task without major difficulties and provide robust and regular data: the average rating values vary smoothly with stimulus intensity (Stevens, 1957). This is true whether or not feedback is provided (e.g. Ward & Lockhead, 1970). The second major finding is Stevens' power law stated above. In addition to these first-order results, there are several second-order effects as well.
The sequential effects are of special interest here because they shed light on the dynamics of the rating process. Numerous studies have indicated that the successive trials in a rating experiment are not independent (Ward & Lockhead, 1970; Jesteadt et al., 1977; Petzold, 1981; Schifferstein & Frijters, 1992). The responses, regarded as a time series, show autocorrelational structure. Typically the data are analyzed using multiple regression in which the stimulus St-1 and the response Rt-1 on the preceding trial enter as predictors after the contribution of the current stimulus St has been partialed out. A robust finding is that current responses tend to be contrasted (i.e. negatively correlated) with previous stimuli and assimilated (positively correlated) toward previous responses. Moreover, there is an interaction between the two time-lagged variables St-1 and Rt-1. The assimilation towards the previous response seems to be modulated by the difference between the two consecutive stimuli St-1 and St (Jesteadt et al., 1977; Petzold, 1981). The closer the stimuli, the stronger the assimilation.
Theoretical analysis of the task also invites the hypothesis that some form of memory is involved in the rating process. Consider a trial in a category-rating experiment. The presentation of the stimulus evokes some subjective percept in the participant. The participant is then faced with the problem of communicating this subjective percept using the particular response scale chosen by the experimenter. There is no a priori correspondence between the subjective magnitudes and the response categories. Such correspondence must be established at the beginning of the experiment and then applied consistently until the end. This is a role for memory.
This hypothesis is supported by a study of Ward and Lockhead (1970). The experiment involved 8 sessions on 8 consecutive days. Feedback was provided at the end of each trial. Unbeknown to the participants the feedback was manipulated so that the response categories were associated with different stimuli on different days. This caused systematic shifts in participants' responses.
The thesis of the present paper is that memory plays an important role in category rating and in particular in the transition from internal magnitudes to overt responses. Memory maintains the consistency of responses over periods of hours and even days. Moreover, the hypothesis is that failures to achieve perfect consistency -- manifested as response drifts, sequential effects, and context effects -- are due to the plasticity of the memory system and reflect the dynamics of its operation.
This paper reports the initial steps towards a memory-based theory of category rating. The theory is instantiated in a computational model called ANCHOR and the predictions of the model are compared with empirical data.
The Anchor model makes detailed predictions on a trial-by-trial basis. To estimate the parameters of the model and evaluate its adequacy as a psychological theory one needs empirical data at the same level of granularity. The psychophysical literature cited in the introduction reports aggregate data only and hence falls short of this standard. Therefore, a psychological experiment was carried out. In addition to providing the necessary data, it replicates the sequential effects from the literature and tests the assumption of linearity of the scale of physical length.
Stimulus Material. The stimuli were pairs of white dots presented against black background on a 17-inch AppleVision monitor. The only independent variable in the experiment was the distance between the two dots measured in pixels. The distance used on each trial was drawn independently from a uniform distribution ranging from 250 pixels (80 mm) to 700 pixels (224 mm). The viewing distance was approximately 500 mm. The imaginary segment formed by the dots was always horizontal and was randomized with respect to its absolute horizontal and vertical position on the screen. The stimulus set for each participant was generated and randomized separately. The maximal distance representable on the monitor was 1000 pixels (320 mm). Each dot was roughly circular in shape with a diameter of 16 pixels (5 mm).
Participants: 24 students participated in the experiment to satisfy a course requirement.
Procedure. The participants were asked to rate the "distance between the dots" on a scale ranging from 1 to 9. The participants entered their responses on the numeric keypad of the computer keyboard. Each trial began with a 500 ms beep followed by 3300 ms stimulus presentation followed by 200 ms inter-trial interval. There were 17 demonstration and 450 experimental trials divided into 10 blocks with short rest periods between the blocks. The demonstration presented stimuli of length 275, 325, 375, ..., 625, 675, 625, ..., 275 pixels and the participants were encouraged to practice pressing the keys 1, 2, ..., 8, 9, 8, ..., 1. No feedback was given during the experimental trials. The whole procedure lasted about 40 minutes.
The data are analyzed at the level of individual participants.
Linearity of the Scale. To estimate the exponent of Stevens' power law, a function of the form R = a + k.Sn is fitted to the data of each individual participant. The exponents n range from 1.01 to 1.12 in the sample of 24 participants, with mean 1.06. Thus the exponent is empirically indistinguishable from unity for all participants. (The correlations between the functions S0.95, S1.00, and S1.10 are greater than 0.99 in the domain [250;700].) This suggests that the assumption of linearity of the scale is correct, at least within the precision of measurement.
Overall Accuracy. The linearity of the scale allows the data to be analyzed by simple linear regression of R on S. The squared correlation coefficient R2 is a measure of the accuracy of the respective participant. It ranges from 0.65 to 0.91 for the 24 participants, with mean 0.80 and std.dev. 0.070. In other words, the immediate stimulus accounts for full three quarters of the response variance, sometimes up to 90%.
Response Distributions. Even though the stimuli are uniformly distributed, the responses are not. Figure 2 shows the response distributions for two representative participants. A marked feature of these distributions is the predominance of responses in the middle of the scale at the expense of extreme ones. The response standard deviation ranges from 1.20 to 2.44, with mean 1.96 and s.d. 0.28. For comparison, if the 450 responses were evenly distributed in 9 categories, the standard deviation would be 2.58.
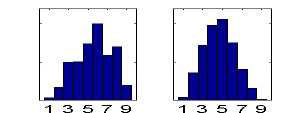
Figure 2. Response distributions for two representative participants.
It seems unlikely that the perceptual subsystem maps the uniform stimulus distribution onto a highly non-uniform distribution of internal magnitudes. Therefore the shape of the response distribution appears to be largely due to the cognitive subsystem. It is possible that the participants reserve the extreme responses for distances that are very short (close to zero) or very long (filling the width of the screen). Such extreme stimuli are not presented during the experiment and this may be one of the reasons for the non-uniformity of responses. However, this explanation does not address the peak in the middle of the scale. The memory-based theory of category rating offers an alternative explanation in terms of self-reinforcing buildup of strength for the frequent responses and corresponding loss of strength for the infrequent ones.
Sequential Effects. A multiple linear regression is performed with the following variables entering as predictors: the current stimulus St, the previous stimulus St-1, and the previous response Rt-1. The signs of the regression coefficients of the time-lagged variables are of special interest. For the previous stimulus St-1, the standardized coefficient betaS ranged from -0.53 to -0.08, with mean -0.25 and s.d. 0.10. Conversely, the standardized coefficient betaR for the previous response Rt-1 ranged from +0.15 to +0.55, with mean +0.30 and s.d. 0.10. Thus all 24 participants without exception show evidence of stimulus-driven contrast and response-driven assimilation.
Additional regression analyses involving interaction terms replicate the finding of Jesteadt et al. (1977) that the assimilation towards Rt-1 is modulated by the difference between the two consecutive stimuli St-1 and St. These analyses are not reported here because of lack of space.
| Next page | > > > | Memory-Based Model of Category Rating |
| [ Back to top ] | |
| [ Petrov's Home Page ][ Petrov's Publications ] | [ Abstract (html) ] |
| [ Anderson's Home Page ][ Anderson's Publications ] | [ PDF file (38K) ] |
| [ ACT-R Main Page ] | [ Slides (127K) ] |