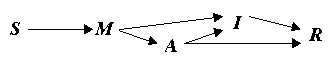
As argued in the introduction, memory seems to play an important role in the category-rating process. The remainder of this paper outlines one particular proposal about the computational mechanisms that may carry out this process. The ANCHOR model proposed here is based on a general theory of memory incorporated in the ACT-R cognitive architecture (Anderson & Lebière, 1998). The ACT-R theory is consistent with a broad range of memory phenomena. Thus Anchor draws a bridge between psychophysics and memory research. The following two subsections describe the model first in general terms and then with details and equations.
The centerpiece of the Anchor model is the construct of an anchor. An anchor is an association between an internal magnitude and a category on the response scale. There is one anchor per category and it can be construed as an internal representation of the prototypical member of this category.
The collection of all anchors defines a mapping from the continuum of magnitudes to the discrete categories of the response scale. This mapping is partly constrained and partly arbitrary. The constraints come from the demand for homomorphism implied by the category-rating task. There is intrinsic ordering of the intensity of the physical stimuli and hence of the magnitudes on the subjective continuum. Also, there is ordering of the response categories. When reporting their subjective magnitudes, the participants try to align the ordering of the two domains.
Another constraint implied by the task is to maintain consistency over time. If, for whatever reason, a stimulus is labeled with a particular response on a given trial, there is pressure to label this stimulus with the same response on subsequent trials. This extends not only to the stimulus that happened to be presented but to other stimuli that evoke similar subjective magnitudes.
These constraints motivate the following mechanisms of the ANCHOR model. When a stimulus is presented and encoded as an internal magnitude, a partial matching mechanism activates an anchor whose magnitude is similar to the magnitude of the target stimulus. In so far as anchor magnitudes are relatively stable, categorization of the stimuli is consistent over time.
The partial matching is stochastic and depends on other factors besides similarity (viz. recency and frequency, discussed below). Therefore it is not guaranteed to retrieve on each trial the anchor that best matches the target magnitude. In the cases when there is large discrepancy between the target magnitude evoked by the stimulus and the anchor magnitude retrieved from memory, a correction mechanism may increment or decrement the response suggested by the anchor. The correction mechanism is stochastic and error-prone too but it does tend to enforce homomorphism between magnitudes and responses.
Phenomenologically, an introspective report of a category-rating trial might run like this, "I see the dots... The distance looks like a 7... No, it's too short for a 7. I'll give it a 6."
So, the stimulus has been encoded, matched against anchors, and a response has been produced. Is this the end of the trial? According to the ANCHOR model and the broader ACT-R theory (Anderson & Lebière, 1998), the answer is no. The cognitive system is plastic (within limits) and each experience seems to leave a mark on it. It is impossible to step into the same river twice. The model postulates an obligatory learning mechanism that pulls the magnitude of the relevant anchor in the direction of the magnitude of the stimulus that has just been presented. Thus each trial results in a slight change of the magnitude of one of the anchors -- namely the one that corresponds to the response given on that particular trial. The notion of obligatory learning is similar to the ideas of Logan (1988), although ANCHOR learns prototypes rather than individual instances.
The implications of this incremental learning mechanism are worth considering in detail. After a long sequence of trials, each anchor magnitude ends up being a weighted average of the magnitudes of all stimuli classified in the corresponding response category. Thus the anchors are true prototypes. However, recent stimuli weigh more heavily than earlier ones, introducing bias. The influence of the initial instructions and demonstrations gradually wash away.
More importantly, the performance of the system on each trial depends on the history of its performance on previous trials. This makes it a dynamic system capable and even forced to exhibit gradual shifts, sequential effects, and self-reinforcing preferences. Each run of the model becomes idiosyncratic in systematic ways apart from the random noise even when tested on the exact same sequence of stimuli.
One final aspect of the model remains to be introduced. There is abundant evidence that the human memory system is sensitive to the frequency and recency of the encoded material. These two factors enter the ACT-R theory and the Anchor model through a construct called base-level activation (BLA). Each memory element, anchors included, has some base-level activation that goes up and down with time. The partial matching mechanism is sensitive not only to the similarity between the target magnitude and the anchor magnitudes but also to the activation levels of the anchors. Overall, anchors with high BLA are more likely to win in the matching process than anchors with low BLA, the target stimulus notwithstanding.
The form of the base-level learning equation (Eq. 6 below) entails that when a response is produced on a trial the BLA of the corresponding anchor receives a sharp transient boost followed by small residual increase. On the other hand, when some response is not used for a long time the activation of the corresponding anchor gradually decays away. In terms of observable behavior, the rapid transient manifests itself as sequential response assimilation and the long-term overall strength leads to rich-gets-richer differentiation of the response frequencies.
Figure 3 shows a schematic diagram of the various quantities used in the model and the dependencies among them.
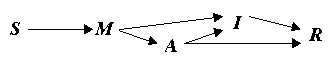
Figure 3. Schematic diagram of the quantities used in the model: physical intensity of the stimulus S, target magnitude M, anchor magnitude A, increment I, and overt response R.
The perceptual subsystem (cf.
Figure 1)
is modeled by a single equation [1].
It transforms the physical intensity of the stimulus
S into an internal magnitude M.
The transformation is linear, with some multiplicative noise.
The magnitudes are arbitrarily scaled between 0.25 and 0.70,
given that S varies between 250 and 700 pixels.
The random variable
![]() is normally distributed with zero mean. Thus the term
(1+
is normally distributed with zero mean. Thus the term
(1+![]() )
is centered around 1.0.
The standard deviation of the noise is a free parameter of
the model. In the simulation experiments reported in the next
section this parameter was set to 0.050.
The multiplicative relationship between the scale value
(i.e. the mean of the magnitude distribution induced by a
given stimulus S) and the noise term implements
Ekman's law (Ekman, 1959).
)
is centered around 1.0.
The standard deviation of the noise is a free parameter of
the model. In the simulation experiments reported in the next
section this parameter was set to 0.050.
The multiplicative relationship between the scale value
(i.e. the mean of the magnitude distribution induced by a
given stimulus S) and the noise term implements
Ekman's law (Ekman, 1959).
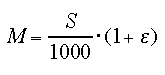 |
[1] |
There are 9 anchors with magnitudes A1 ... A9 respectively. The partial matching mechanism has to select one of them according to their similarity to the target magnitude M and their base-level activations B1 ... B9. This process is governed by two equations. First, a score is produced for each anchor according to Equation 2. Second, one anchor is chosen according to the softmax Equation 3.
|
|
[2] |
The mismatch (or dissimilarity) between two magnitudes is simply the absolute difference between them. The mismatch is multiplied by a mismatch penalty factor MP and subtracted from the base-level activation of the anchor to produce the combined score for this anchor. MP is a free parameter of the model that scales the mismatches relative to the activation values. It was set to 7.0 in the simulations.
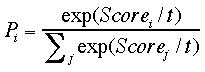 |
[3] |
Equation 3 converts scores into retrieval probabilities. Pi is the probability of retrieval of anchor i and exp(·) denotes the exponentiation function. The temperature t is a free parameter of the model controlling the degree of non-determinism of the partial-matching process. It was set to 0.40 in the simulations.
Having retrieved an anchor, the model has to determine the correction I to produce the final response. Under the current settings of the model, the correction can be 0, +/-1, and occasionally +/-2. The correction depends, stochastically, on the discrepancy between the target magnitude M and the anchor magnitude A. One free parameter of the model -- d -- defines a set of five discrepancy reference points {-2d, -d, 0, d, 2d}. They are compared with the algebraic difference (M-A) to produce correction scores:
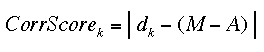 |
[4] |
The correction scores are converted to choice probabilities by an equation analogous to Equation 3. The only differences are that the correction scores enter with negative signs, thus transforming the softmax rule into softmin, and that a separate temperature parameter is used. In the simulations this parameter was set to 0.040. The discrepancy reference parameter was d=0.090. To illustrate these settings, suppose the anchor magnitude A is 0.050 below the target magnitude M, which is roughly the width of one response category. Then there is 51% chance that the model will increment the anchor response by +1, 39% chance to leave it unchanged, and marginal chance to increment it by +2 or decrement it.
The final response R is the algebraic sum of the anchor label and the increment, clipped between 1 and 9 if needed.
At the end of the trial the learning mechanism updates the
magnitude of the anchor corresponding to the response
R. (Note that this does not necessarily coincide
with the anchor retrieved from memory.)
The anchor magnitude A is updated according to
Equation 5,
which is a form of competitive learning. The learning rate
![]() weighs the most recent trial relative to earlier ones.
The simulation experiments used
weighs the most recent trial relative to earlier ones.
The simulation experiments used
![]() =0.50.
=0.50.
|
|
[5] |
The base-level learning equation is somewhat less transparent. The ACT-R theory postulates Equation 6a which contains an explicit term for each instant the anchor is updated (Anderson & Lebière, 1998, p.124). Suppose a particular response has been given at time lags t1 ... tn from the present trial. Then the base-level activation B of the corresponding anchor is the logarithm of a sum of powers [6a], where d is a decay parameter.
![B=ln[sum(t_i^-d)]](eq6a.gif) |
[6a] |
Because Equation 6a is computationally expensive, the model uses Equation 6b which closely approximates the theoretical formula. The approximation disregards the detailed update history and retains only the time lag since the last usage t, the lag T since the beginning of the experiment, and the total number of times the corresponding response has been given up to the current trial. In the simulation experiments the decay parameter was set to d=0.5, which is a default value used in many ACT-R models. The duration of each trial was 4 sec, as in the psychological experiment.
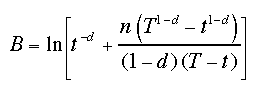 |
[6b] |
Equations 2, 3, 4, and 6a are taken verbatim from the ACT-R architecture (Anderson & Lebière, 1998) and thus establish continuity between the Anchor model and a broad spectrum of memory-related models. Equation 1 is ANCHOR's connection to Stevens' and Ekman's psychophysical laws.
| Next page | > > > | Evaluation of the model |
| Previous page | > > > | Introduction |
| [ Back to top ] | |
| [ Petrov's Home Page ][ Petrov's Publications ] | [ Abstract (html) ] |
| [ Anderson's Home Page ][ Anderson's Publications ] | [ PDF file (38K) ] |
| [ ACT-R Main Page ] | [ Slides (127K) ] |